簡介
偏差是相對於中位數來衡量,而非相對於均值(期望值),在這種情況下為了與通常的 均值無偏性區別,稱作 中值無偏。偏差與一致性相關聯,一致估計量都是收斂並且 漸進無偏的(因此會收斂到正確的值),雖然一致序列中的個別估計量可能是有偏的(只要偏差收斂於零) 。
當其他量相等時,無偏估計量比有偏估計量更好一些,但在實踐中,並不是所有其他統計量的都相等,於是也經常使用有偏估計量,一般偏差較小。當使用一個有偏估計量時,也會估計它的偏差。有偏估計量可能用於以下原因:由於如果不對總體進一步假設,無偏估計量不存在或很難計算(如標準差的無偏估計);由於估計量是中值無偏的,卻不是均值無偏的(或反之);由於一個有偏估計量較之無偏估計量(特別是收縮估計量)可以減小一些損失函式(尤其是均方差);或者由於在某些情況下,無偏的條件太強,而這些無偏估計量沒有太大用處。此外,在非線性變換下均值無偏性不會保留,不過中值無偏性會保留;例如樣本方差是總體方差的無偏估計量,但它的平方根標準差則是總體標準差的有偏估計量。
定義
 有偏估計
有偏估計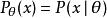 有偏估計
有偏估計 有偏估計
有偏估計 有偏估計
有偏估計 有偏估計
有偏估計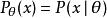 有偏估計
有偏估計 有偏估計
有偏估計 有偏估計
有偏估計 有偏估計
有偏估計 有偏估計
有偏估計設我們有一個參數為實數 的機率模型,產生觀測數據的機率分布 ,而統計量 是基於任何觀測數據 下 的估計量。也就是說,我們假定我們的數據符合某種未知分布 (其中 是一個固定常數,而且是該分布的一部分,但具體值未知),於是我們構造估計量 ,該估計量將觀測數據與我們希望的接近 的值對應起來。因此這個估量的(相對於參數 的) 偏差定義為
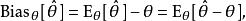 有偏估計
有偏估計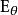 有偏估計
有偏估計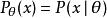 有偏估計
有偏估計 有偏估計
有偏估計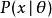 有偏估計
有偏估計其中 表示分布 的期望值,即對所有可能的觀測值 取平均。由於 θ對於條件分布 是可測的,就有了第二個等號。
對於參數 θ的所有值的偏差都等於零的估計量稱為 無偏估計。
在一次關於估計量性質的模擬實驗中, 有偏估計可以用平均有符號離差來評估。
樣本方差
隨機變數的樣本方差從兩方面說明了估計量偏差:首先,自然估計量(naive estimator)是有偏的,可以通過比例因子校正;其次,無偏估計量的均方差(MSE)不是最優的,可以用一個不同的比例因子來最小化,得到一個比無偏估計量的MSE更小的有偏估計量。
 有偏估計
有偏估計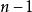 有偏估計
有偏估計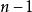 有偏估計
有偏估計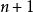 有偏估計
有偏估計具體地說,自然估計量就是將離差平方和加起來然後除以 ,是有偏的。不過除以 會得到一個無偏估計量。相反,MSE可以通過除以另一個數來最小化(取決於分布),但這會得到一個有偏估計量。這個數總會比 大,所以這就叫做收縮估計量,因為它把無偏估計量向零“收縮”;對於常態分配,最佳值為 。
 有偏估計
有偏估計 有偏估計
有偏估計 有偏估計
有偏估計設 期望為 、方差為 的獨立同分布隨機變數。如果樣本均值與未修正樣本方差定義為
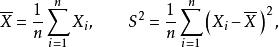 有偏估計
有偏估計 有偏估計
有偏估計 有偏估計
有偏估計則 是 的一個有偏估計量,因為
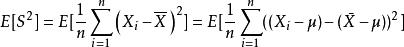 有偏估計
有偏估計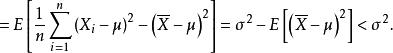 有偏估計
有偏估計 有偏估計
有偏估計 有偏估計
有偏估計換句話說,未修正的樣本方差的期望值不等於總體方差 ,除非乘以歸一化因子。而樣本均值是總體均值 的無偏估計量。
 有偏估計
有偏估計 有偏估計
有偏估計 有偏估計
有偏估計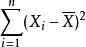 有偏估計
有偏估計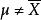 有偏估計
有偏估計是有偏的原因源於樣本均值是的普通最小二乘(OLS)估計量這個事實: 是令 儘可能小的數。也就是說,當任何其他數代入這個求和中時,這個和只會增加。尤其是,在選取 就會得出,
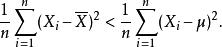 有偏估計
有偏估計於是,
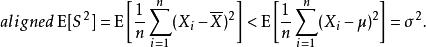 有偏估計
有偏估計注意到,通常的樣本方差定義為
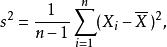 有偏估計
有偏估計而這時總體方差的無偏估計量。可以由下式看出:
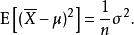 有偏估計
有偏估計有偏(未修正)與無偏估計之比稱為貝塞爾修正 。
