定義
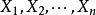 無偏估計量
無偏估計量設 是來自總體X的一個樣本,θ是包含在總體X的分布中的待估參數。
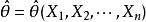 無偏估計量
無偏估計量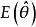 無偏估計量
無偏估計量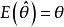 無偏估計量
無偏估計量 無偏估計量
無偏估計量若估計量 的數學期望 存在,且有 ,則稱 是θ的無偏估計量。
實際意義
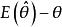 無偏估計量
無偏估計量 無偏估計量
無偏估計量在科學技術中, 稱為以 作為θ的估計的系統誤差,無偏估計的實際意義就是無系統誤差。
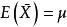 無偏估計量
無偏估計量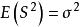 無偏估計量
無偏估計量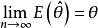 無偏估計量
無偏估計量 無偏估計量
無偏估計量例如,設總體X的均值及方差σ²都存在但均未知,因為 , ,這就是說不論總體服從什麼分布,其樣本均值是總體均值的無偏估計,樣本方差是總體方差的無偏估計。若 ,則稱 是θ的漸進無偏估計量。
結論
結論一
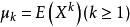 無偏估計量
無偏估計量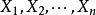 無偏估計量
無偏估計量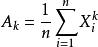 無偏估計量
無偏估計量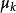 無偏估計量
無偏估計量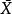 無偏估計量
無偏估計量設總體X的k階中心矩 存在, 是X的一個樣本,不論X服從什麼分布, 是 的無偏估計量。特別地,不論X服從什麼分布,只要E(X)存在, 總是E(X)的無偏估計。
證明
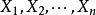 無偏估計量
無偏估計量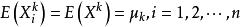 無偏估計量
無偏估計量因為 與X同分布,所以 。
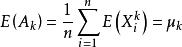 無偏估計量
無偏估計量結論二
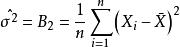 無偏估計量
無偏估計量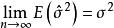 無偏估計量
無偏估計量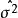 無偏估計量
無偏估計量對於總體X,設E(X)=,D(X)=σ²都存在,且σ²>0,若,σ²均未知,則σ²的估計量 是有偏的。另一方面,由於 ,所以 是σ²的漸進無偏估計量。
證明
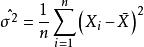 無偏估計量
無偏估計量因為,而
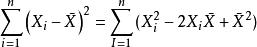 無偏估計量
無偏估計量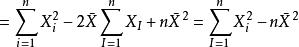 無偏估計量
無偏估計量故
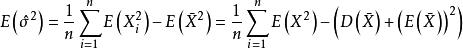 無偏估計量
無偏估計量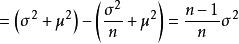 無偏估計量
無偏估計量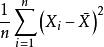 無偏估計量
無偏估計量所以是σ²的有偏估計。
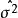 無偏估計量
無偏估計量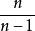 無偏估計量
無偏估計量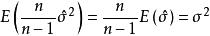 無偏估計量
無偏估計量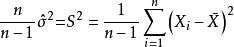 無偏估計量
無偏估計量若在的兩邊同乘,即,而。
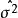 無偏估計量
無偏估計量可見樣本方差S²可以作為方差σ²的估計,而且是無偏估計。因此常用S²作為方差σ²的估計量。從無偏估計量的角度考慮,S²比二階中心矩作為的估計好。
套用
 無偏估計量
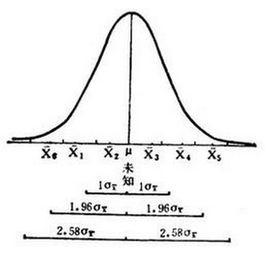
無偏估計量在實際套用中,對整個系統(整個實驗)而言無系統偏差,就一次實驗來講, 可能偏大也可能偏小,實質上並說明不了什麼問題,只是平均來說它沒有偏差,所以無偏性只有在大量的重複實驗中才能體現出來;另一方面,無偏估計只涉及一階矩(均值),雖然計算簡便,但往往會出現一個參數的無偏估計有多個,而無法確定哪個估計量好。因此,無偏性的作用在於可以把重複估計中的各次誤差通過平均來消除。這並不意味著該估計量在一次使用時並能獲得良好的結果。在具體問題中,無偏性是否合理,應當結合具體情況來考慮。在有些問題中,無偏性的要求可能會導出不同的結果來。
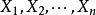 無偏估計量
無偏估計量事實上, 中的每一個均可作為θ的無偏估計量,究竟哪個估計量更合理,就看哪個估計量的觀察值更接近真實值,即估計量的觀察值更密集地分布在真實值附近。而方差能反映隨機變數取值的分散程度,所以無偏估計以方差最小者為最好、最合理,為此後人引進了估計量的有效性概念。