定義
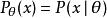 估計誤差
估計誤差 估計誤差
估計誤差 估計誤差
估計誤差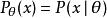 估計誤差
估計誤差 估計誤差
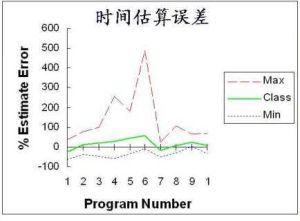
估計誤差設我們有一個參數為實數 θ的機率模型,產生觀測數據的機率分布 ,而統計量 是基於任何觀測數據 下 θ的估計量。也就是說,我們假定我們的數據符合某種未知分布 (其中 θ是一個固定常數,而且是該分布的一部分,但具體值未知),於是我們構造估計量 ,該估計量將觀測數據與我們希望的接近 θ的值對應起來。因此這個估量的(相對於參數 θ的) 誤差定義為
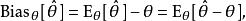 估計誤差
估計誤差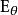 估計誤差
估計誤差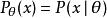 估計誤差
估計誤差 估計誤差
估計誤差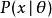 估計誤差
估計誤差其中 表示分布 的期望值,即對所有可能的觀測值 取平均。由於 θ對於條件分布 是可測的,就有了第二個等號。
對於參數 θ的所有值的誤差都等於零的估計量稱為無偏估計量。
在一次關於估計量性質的模擬實驗中,估計量的偏差可以用平均有符號離差來評估。
誤差的分類
根據誤差的性質和產生的原因,可將誤差分為
系統誤差、隨機誤差、過失誤差三類。
(1)系統誤差
系統誤差是由某些固定不便的因素引起的,這些因素影響的結果永遠朝一個方向偏移,其大小及符號在同一組實驗測量中完全相同。當實驗條件一經確定,系統誤差就是一個客觀上的恆定值,多次測量的平均值也不能減弱它的影響。誤差隨實驗條件的改變按一定規律變化。產生系統誤差的原因有以下幾方面:
①測量儀器方面的因素,如儀器設計上的缺點,刻度不準,儀表未進行校正或標準表本身存在偏差,安裝不正確等;
②環境因素,如外界溫度、濕度、壓力等引起的誤差;
③測量方法因素,如近似的測量方法或近似的計算公式等引起的誤差;
④測量人員的習慣和偏向或動態測量時的滯後現象等,如讀數偏高或偏低所引起的誤差。針對以上具體情況分別改進儀器和實驗裝置以及提高測試技能予以解決。
(2)隨機誤差
它是由某些不易控制的因素造成的。
在相同條件下做多次測量,其誤差數值是不確定的,時大時小,時正時負,沒有確定的規律,這類誤差稱為隨機誤差或偶然誤差。
這類誤差產生原因不明,因而無法控制和補償。
若對某一量值進行足夠多次的等精度測量,就會發現隨機誤差服從統計規律,誤差的大小或正負的出現完全由機率決定的。
隨著測量次數的增加,隨機誤差的算術平均值趨近於零,所以多次測量結果的算術平均值將更接近於真值。
(3)過失誤差
過失誤差是一種與實際事實明顯不符的誤差,誤差值可能很大,且無一定的規律。
它主要是由於實驗人員粗心大意、操作不當造成的,如讀錯數據,操作失誤等。在測量或實驗時,只要認真負責是可以避免這類誤差的。存在過失誤差的觀測值在實驗數據整理時應該剔除。
(4)精密度和精確度
測量的質量和水平可以用誤差概念來描述,也可以用精確度來描述。為了指明誤差來源和性質,可分為精密度精和精確度。
精密度:在測量中所測得的數值重現性的程度。它可以反映隨機誤差的影響程度,隨機誤差小,則精密度高。
精確度:測量值與真值之間的符合程度。它反映了測量中所有系統誤差和隨機誤差的綜合。
精密度和精確度分為A、B、C三檔
A的系統誤差大,隨機誤差大,精密度、精確度都不好;
B說明系統誤差大,隨機誤差小,精密度很好,但精確度不好;
C系統誤差和隨機誤差都很小,精密度和精確度都很好。
(5)實驗數據的記數法和有效數字
實驗測量中所使用的儀器儀表只能達到一定的精度,因此測量或運算的結果不可能也不應該超越儀器儀表所允許的精度範圍。
估計誤差量化
在統計學中, 估計量是基於觀測數據計算一個已知量的估計值的法則估計量用來估計未知總體的參數。對於給定的參數,可以有許多不同的估計量。我們通過一些選擇標準從它們中選出較好的估計量,但是有時候很難說選擇這一個估計量比另外一個好 。
1.誤差
 估計誤差
估計誤差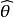 估計誤差
估計誤差對於一個給定樣本,估計量的"誤差"定義為
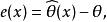 估計誤差
估計誤差 估計誤差
估計誤差其中是待估參數。注意誤差 e不僅取決於估計量(估計公式或過程),還取決於樣本。
2.均方誤差
 估計誤差
估計誤差估計量的均方誤差被定義為誤差的平方的期望值,即為:
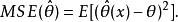 估計誤差
估計誤差它用來顯示估計值的集合與被估計單個參數的平均差異。試想下面的類比:假設“參數”是靶子的靶心,“估計量”是向靶子射箭的過程,而每一支箭則是“估計值”(樣本)。那么,高均方誤差就意味著每一支箭離靶心的平均距離較大,低均方誤差則意味著每一支箭離靶心的平均距離較小。箭支可能集聚,也可能不。比如說,即使所有箭支都射中了同一個點,同時卻嚴重偏離了靶子,均方誤差相對來說依然很大。然而要注意的是,如果均方誤差相對較小,箭支則更有可能集聚(而不是離散)。
3.抽樣偏差
4.方差
5.偏差
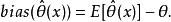 估計誤差
估計誤差舉例
例1.樣本方差:
隨機變數的樣本方差從兩方面說明了估計量偏差:首先,自然估計量(naive estimator)是有偏的,可以通過比例因子校正;其次,無偏估計量的均方差(MSE)不是最優的,可以用一個不同的比例因子來最小化,得到一個比無偏估計量的MSE更小的有偏估計量。具體地說,自然估計量就是將離差平方和加起來然後除以 n,是有偏的。不過除以 n−1 會得到一個無偏估計量。相反,MSE可以通過除以另一個數來最小化(取決於分布),但這會得到一個有偏估計量。這個數總會比 n−1 大,所以這就叫做收縮估計量,因為它把無偏估計量向零“收縮”;對於常態分配,最佳值為 n+1 。
設 X, ..., X是期望為 μ、方差為 σ的獨立同分布(i.i.d.)隨機變數。如果樣本均值與未修正樣本方差定義為
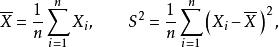 估計誤差
估計誤差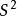 估計誤差
估計誤差 估計誤差
估計誤差則是的一個有偏估計量,
因為
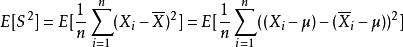 估計誤差
估計誤差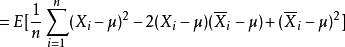 估計誤差
估計誤差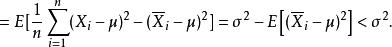 估計誤差
估計誤差換句話說,未修正的樣本方差的期望值不等於總體方差 σ,除非乘以歸一化因子。而樣本均值是總體均值 μ的無偏估計量。
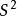 估計誤差
估計誤差 估計誤差
估計誤差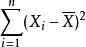 估計誤差
估計誤差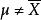 估計誤差
估計誤差是有偏的原因源於樣本均值是 μ的普通最小二乘(OLS)估計量這個事實:是令儘可能小的數。也就是說,當任何其他數代入這個求和中時,這個和只會增加。尤其是,在選取就會得出,
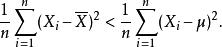 估計誤差
估計誤差於是,
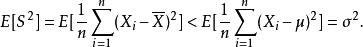 估計誤差
估計誤差注意到,通常的樣本方差定義為
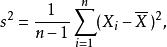 估計誤差
估計誤差而這時總體方差的無偏估計量。可以由下式看出:
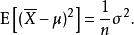 估計誤差
估計誤差方差的有偏(未修正)與無偏估計之比稱為貝塞爾修正。