原理介紹
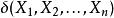 最小方差無偏估計
最小方差無偏估計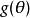 最小方差無偏估計
最小方差無偏估計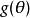 最小方差無偏估計
最小方差無偏估計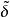 最小方差無偏估計
最小方差無偏估計若為參數函式的一個無偏估計,且對於參數函式的任一無偏估計恆有下列關係
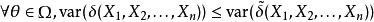 最小方差無偏估計
最小方差無偏估計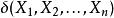 最小方差無偏估計
最小方差無偏估計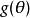 最小方差無偏估計
最小方差無偏估計則稱為參數函式的一致最小方差無偏估計(UMVUE)。
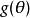 最小方差無偏估計
最小方差無偏估計若參數函式
存在無偏估計,則可證明出一致最小方差無偏估計存在且只有一個。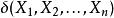 最小方差無偏估計
最小方差無偏估計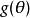 最小方差無偏估計
最小方差無偏估計 最小方差無偏估計
最小方差無偏估計一般地,設是參數函式的無偏估計且統計量是分布族的完備充分統計量,則
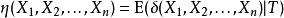 最小方差無偏估計
最小方差無偏估計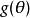 最小方差無偏估計
最小方差無偏估計是參數函式的一致最小方差無偏估計(UMVUE)。
評估器選擇
不需要存在有效的估計量,但如果確實如此,並且如果它是無偏的,那么它就是MVUE。 由於估計量δ的均方誤差(MSE)是
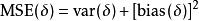 最小方差無偏估計
最小方差無偏估計MVUE使無偏估計中的MSE最小化。 在某些情況下,偏差估計量的MSE較低,因為它們的方差小於任何無偏估計量。
例子
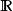 最小方差無偏估計
最小方差無偏估計考慮將數據作為單個觀察,來自上具有密度的絕對連續分布
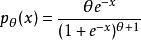 最小方差無偏估計
最小方差無偏估計我們希望找到UMVU的估算器
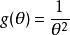 最小方差無偏估計
最小方差無偏估計首先,我們了解到密度可以寫成
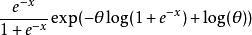 最小方差無偏估計
最小方差無偏估計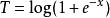 最小方差無偏估計
最小方差無偏估計 最小方差無偏估計
最小方差無偏估計這是一個指數族,具有足夠的統計量。實際上這是一個滿秩指數族,因此足夠完整。
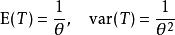 最小方差無偏估計
最小方差無偏估計因此,
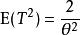 最小方差無偏估計
最小方差無偏估計在這裡,我們使用Lehmann-Scheffé定理得到MVUE
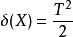 最小方差無偏估計
最小方差無偏估計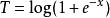 最小方差無偏估計
最小方差無偏估計顯然是無偏並且足夠完整,因此UMVU估算器是
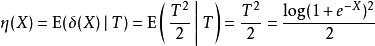 最小方差無偏估計
最小方差無偏估計這個例子說明了完整的充分統計量的無偏函式將是UMVU,正如Lehmann-Scheffé定理所述。
其它例子
對於具有未知均值和方差的常態分配,樣本均值和(無偏)樣本方差是總體均值和總體方差的MVUE。
然而,樣本標準偏差對於總體標準偏差不是無偏的。
此外,對於其他分布,樣本均值和樣本方差通常不是MVUE - 對於具有未知上限和下限的均勻分布,中間範圍是總體均值的MVUE。
如果在具有未知上限N的集合{1,2,...,N}上從離散均勻分布中選擇k個樣本(沒有替換),則N的MVUE是
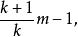 最小方差無偏估計
最小方差無偏估計其中m是樣本最大值。 這是樣本最大值的縮放和移位(如此無偏)變換,這是一個足夠和完整的統計量。

