基本介紹
統計估計是指推斷統計中用樣本資料去估計總體參數的方法。有 點估計與 區間估計兩種。
數理統計包括 統計描述和 統計推斷兩部分,統計推斷就是由樣本推斷總體,是統計學的核心內容,統計推斷內容非常豐富,大致可以歸納為兩大類: 統計估計和 統計檢驗。統計估計分為 參數估計和非參數估計、點估計和區間估計,下面只涉及參數的點估計和區間估計,參數的點估計,指用樣本統計量的值估計未知參數的值。參數的區間估計就是用樣本來確定一個區間,使這個區間以很大的機率包含所估計的未知參數,這樣的區間稱為置信區間 。
點估計
點估計是直接估計總體參數的值,通常用樣本數據的一個統計量作為總體參數的估計量。例如,在估計一個正態總體的平均數時,把樣本數據的平均數取作總體平均數的估計量。點估計時,要求樣本統計量是無偏統計量,即要求在無數次重複抽樣時,這種樣本統計量產生的分布的平均數等於被估計的參數。還要求這個樣本分布的方差比其他無偏估計量的方差要小 。
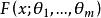 統計估計
統計估計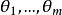 統計估計
統計估計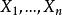 統計估計
統計估計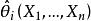 統計估計
統計估計 統計估計
統計估計 統計估計
統計估計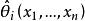 統計估計
統計估計 統計估計
統計估計若總體X的分布函式 的類型已知,其中的參數 是未知的,這時可以在總體X中抽取樣本 ,根據待估參數的特徵構造出適當的統計量 作為參數 的估計量;然後由抽取的樣本觀察值 ,計算得到估計量的觀察值 ,就是未知參數 的估計值(i=1,2,…,m),這種做法稱為 參數的點估計,常用的點估計方法有 矩估計和 最大似然估計,對估計量優劣的評價標準有 無偏性、 有效性和 一致性( 相合性)等 。
矩估計法
矩估計法的基本思想是:用樣本矩估計總體矩,用樣本矩的函式去估計總體矩的相應的函式,從而達到對總體參數進行估計的目的。
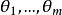 統計估計
統計估計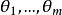 統計估計
統計估計總體X分布的參數 往往通過總體矩(數字特徵)反映出來,因此若用樣本矩來替換總體矩,用樣本矩的函式替換相應的總體矩的函式,則可獲得總體參數 的估計量,這種估計方法稱為矩估計法 。
最大似然估計
 統計估計
統計估計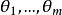 統計估計
統計估計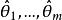 統計估計
統計估計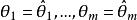 統計估計
統計估計 統計估計
統計估計最大似然估計又稱 極大似然估計,它的基本思想是在給定樣本觀察值 之下,給出參數 的估計值 ,使得在 之下,樣本 出現的可能性最大 .
估計量的概念及評價標準
 統計估計
統計估計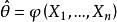 統計估計
統計估計 統計估計
統計估計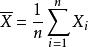 統計估計
統計估計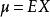 統計估計
統計估計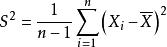 統計估計
統計估計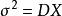 統計估計
統計估計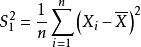 統計估計
統計估計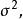 統計估計
統計估計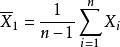 統計估計
統計估計 統計估計
統計估計用來估計未知參數 的真值的統計量 稱為 的 估計量,如用 作為總體期望 的估計量,用 作總體方差 的估計量等等,但也可用 估計 用 估計 等,也就是說估計量不唯一,因而存在對估計量的評價問題,評價標準主要有三條:
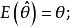 統計估計
統計估計(1) 無偏性 即
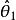 統計估計
統計估計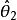 統計估計
統計估計 統計估計
統計估計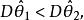 統計估計
統計估計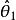 統計估計
統計估計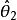 統計估計
統計估計 統計估計
統計估計 統計估計
統計估計 統計估計
統計估計 統計估計
統計估計(2) 有效性(最小方差性) 若 和 都是 的無偏估計量,如果 則稱 比 有效。若在 的一切無偏估計中, 的方差最小,稱 為 的最小方差無偏估計量;
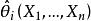 統計估計
統計估計 統計估計
統計估計 統計估計
統計估計 統計估計
統計估計 統計估計
統計估計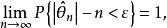 統計估計
統計估計 統計估計
統計估計 統計估計
統計估計(3) 一致性(相合性) 設是的估計量,若依機率收斂於,即對任意,有則稱是的 一致估計量>常用估計量都滿足一致性,所以我們在評價估計量時,往往只驗證其無偏性與其比較有效性 。
區間估計
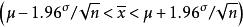 統計估計
統計估計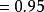 統計估計
統計估計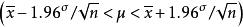 統計估計
統計估計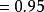 統計估計
統計估計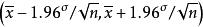 統計估計
統計估計區間估計是構造 一個區間,推斷參數的真值以某個機率落在這個區間內。這個機率稱為“ 區間的置信水平”。這個區間,稱為“ 置信區間”。例如已知一個常態分配,它的平均數為μ,方差為α 。反覆抽取數據個數為n的樣本直至無數次,由中心極限定理可知,這些樣本的平均數x形成一個以總體平均數μ為平均數。方差為α /n的常態分配。根據常態分配性質,對任意 一個樣本的平均數x,可有 的機率。 這個關係完全等價於 的機率。 總體平均數是未知的,x的值可以從我們抽取的某個樣本中求出,則從上式推斷總體平均數μ將在0.95的機率水平上落在區間 內, 這就是總體平均數的置信區間。在這區間的上下限中,總體的方差α 一般也是未知的,我們仍要用樣本資料對它進行點估計,並在實際構造置信區間時,不一定用常態分配而用t分布等其他分布,使得推斷更為可靠 。

