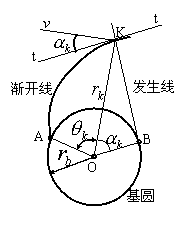
 漸開線齒廓
漸開線齒廓如圖,直線BK沿半徑為
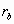 漸開線齒廓
漸開線齒廓基圓:半徑為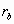 的圓
的圓
基圓半徑: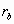
漸開線的發生線:直線BK
K點的展角:
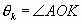 漸開線齒廓
漸開線齒廓漸開線性質
1、發生線在基圓上滾過的長度
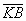 漸開線齒廓
漸開線齒廓即 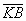 =AB
=AB
2、漸開線上離基圓越遠的部分,其曲率半徑越大,漸開線越平直。
發生線BK與基圓的切點B是漸開線在K的曲率中心,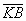 是相應的曲率半徑,漸開線上離基圓越遠的部分,其曲率半徑越大,漸開線越平直;漸開線上離基圓越近的部分,其曲率半徑越小,漸開線越彎曲;漸開線在基圓上起始點處的曲率半徑為零。
是相應的曲率半徑,漸開線上離基圓越遠的部分,其曲率半徑越大,漸開線越平直;漸開線上離基圓越近的部分,其曲率半徑越小,漸開線越彎曲;漸開線在基圓上起始點處的曲率半徑為零。
3、漸開線上任一點的法線恆與基圓相切
發生線BK沿基圓作純滾動,發生線恆切於基圓;發生線與基圓的切點B為其速度瞬心,故發生線BK為漸開線又是K點的法線。
4、基圓內無漸開線
5、漸開線的形狀取決於基圓的大小
基圓越小,漸開線越彎曲;基圓越大,漸開線越平直;當基圓半徑為無窮大時,漸開線將成為一條直線。
漸開線方程
1、壓力角:當用漸開線作齒輪的齒廓時,齒廓上點K速度方向
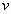 漸開線齒廓
漸開線齒廓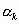 漸開線齒廓
漸開線齒廓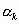 =
=
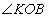 漸開線齒廓
漸開線齒廓漸開線上點的位置不同,壓力角不同。
2、漸開線方程
以O為極點,以OA為極軸,建立漸開線的極坐標方程:
向徑:
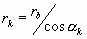 漸開線齒廓
漸開線齒廓極角:
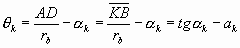 漸開線齒廓
漸開線齒廓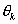 漸開線齒廓
漸開線齒廓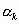 的漸開線函式,用
的漸開線函式,用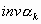 漸開線齒廓
漸開線齒廓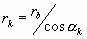 漸開線齒廓
漸開線齒廓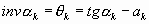 漸開線齒廓
漸開線齒廓嚙合特性
1、嚙合線為一條直線
不論兩齒廓在任何位置接觸,其嚙合點的公法線
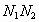 漸開線齒廓
漸開線齒廓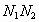 就稱為嚙合線。
就稱為嚙合線。優點:漸開線齒輪傳動過程中,齒廓間的正壓力方向始終不變,對齒輪傳動平穩性極為有利。
2、能實現定傳動比傳動
不論兩齒廓在任何位置接觸,嚙合線是一條定直線,其與連心線的交點C必為一定點,所以能實現定傳動比傳動。
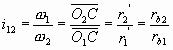 漸開線齒廓
漸開線齒廓相關詞條
參考文獻
[1]、《機械原理》高等教育出版社
