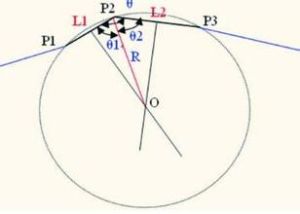
定義
曲線的曲率。平面曲線的曲率就是針對曲線上某個點的切線方向角對弧長的轉動率，通過微分來定義，表明曲線偏離直線的程度。K=lim|Δα/Δs|，Δs趨向於0的時候，定義k就是曲率。
如果在某條曲線上的某個點可以找到一個相對的圓形跟他有相等的曲率,
那么曲線上這個點的曲率半徑就是該圓形的半徑（注意,是這個點的曲率半徑,其他點有其他的曲率半徑).也可以這樣理解：就是把那一段曲線儘可能的微分，直到最後近似一個圓弧，這個圓弧對應的半徑即曲線上這個點的曲率半徑.
公式推導
ρ=|[(1+y'^2)^(3/2)]/y"|，證明如下：一般稱為曲線在某一點的曲率半徑。幾何意義為在該點做曲線的法線（在凹的一側），在法線上取圓心，以ρ為半徑做圓，則此圓稱為該點處的曲率圓。曲率圓與該點有相同的曲率，切線及一階、兩階稻樹。
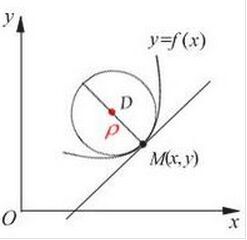曲率半徑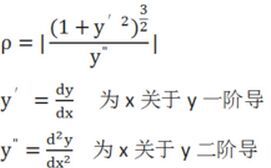
曲率半徑推導解析
曲線上某點的曲率半徑是該點的密切圓（Osculatingcircle）的半徑。密切圓可能是與曲線在該點相內切的圓中半徑最大的（比如在橢圓長軸頂點處），也可能是與曲線在該點相外切的圓中半徑最小的（比如在橢圓短軸頂點處），也可能兩者都不是。比如對於直線上任一點，和直線在該點相切的圓的半徑可以任意大，所以直線的曲率半徑為無窮大（對應於曲率為零，也就是“不彎曲”）。
而在圓上，每一點的密切圓就是其本身，故其曲率半徑為其本身的半徑。
拋物線頂點曲率半徑為焦準距（頂點到焦點距離的兩倍）。
對於y=f(x),曲率半徑等於(1+(f')^2)^(3/2)/|f"|。
