定義
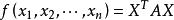 正定二次型
正定二次型 正定二次型
正定二次型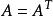 正定二次型
正定二次型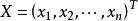 正定二次型
正定二次型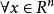 正定二次型
正定二次型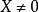 正定二次型
正定二次型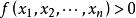 正定二次型
正定二次型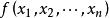 正定二次型
正定二次型 正定二次型
正定二次型設 ,其中矩陣 是對稱陣,即 , 為列向量,若 , ,有 ,則稱為正定二次型,稱實對稱矩陣 正定。
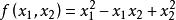 正定二次型
正定二次型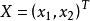 正定二次型
正定二次型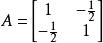 正定二次型
正定二次型例如,即為正定二次型,其中,。
性質
 正定二次型
正定二次型 正定二次型
正定二次型(1) 階實對稱矩陣 正定
 正定二次型
正定二次型 正定二次型
正定二次型 正定二次型
正定二次型的正慣性指數等於
 正定二次型
正定二次型 正定二次型
正定二次型與單位矩陣契約
 正定二次型
正定二次型 正定二次型
正定二次型的順序主子式大於零
 正定二次型
正定二次型 正定二次型
正定二次型的特徵值大於零
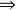 正定二次型
正定二次型 正定二次型
正定二次型的行列式大於零(但行列式大於零的矩陣不一定是正定矩陣)
 正定二次型
正定二次型 正定二次型
正定二次型 正定二次型
正定二次型 正定二次型
正定二次型(2)若 階實對稱矩陣 和 正定, 為實數,則
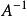 正定二次型
正定二次型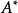 正定二次型
正定二次型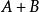 正定二次型
正定二次型① (逆)、 (伴隨矩陣)、 均正定;
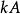 正定二次型
正定二次型 正定二次型
正定二次型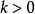 正定二次型
正定二次型② 正定 ;
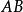 正定二次型
正定二次型 正定二次型
正定二次型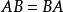 正定二次型
正定二次型③ 正定
判定方法
判定二次型(或對稱矩陣)為正定的方法有如下兩種
行列式法
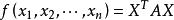 正定二次型
正定二次型對於給定的二次型,寫出它的矩陣,根據對稱矩陣的所有順序主子式是否全大於零來判定二次型 (或對稱矩陣)的正定性。
正慣性指數法
 正定二次型
正定二次型對於給定的二次型 ,先將化為標準形,然後根據標準形中平方項係數為正的個數是否等於來判定二次型的正定性。
 正定二次型
正定二次型通過正交變換,將二次型化為標準形後,標準形中平方項的係數就是二次型矩陣的特徵值。因此,可先求二次型矩陣的特徵值,然後根據大於零的特徵值個數是否等於來判定二次型的正定性。

