介紹
 二次空間
二次空間二次型是 個變數上的二次齊次多項式。下面給出一個、兩個、和三個變數的二次形式:
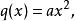 二次空間
二次空間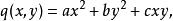 二次空間
二次空間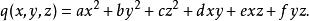 二次空間
二次空間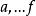 二次空間
二次空間其中 是係數。注意一般的二次函式和二次方程不是二次形式的例子,因為它們不總是齊次的 。
 二次空間
二次空間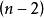 二次空間
二次空間任何非零的 維二次形式定義在投影空間中一個 維的投影空間。在這種方式下可把3維二次形式可視化為圓錐曲線。
 二次空間
二次空間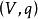 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間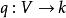 二次空間
二次空間術語 二次空間也經常用來提及 二次型,它是有序對 ,這裡的 是在域 上的向量空間,而 是在 上的二次形式。例如,在三維歐幾里得空間中兩個點之間的距離可以採用涉及六個變數的二次形式的平方根來找到,它們是這兩個點的各自的三個坐標。
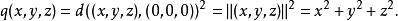 二次空間
二次空間定義
 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間設是在交換環上的模;經常是域比如實數,在這種情況下是向量空間。
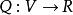 二次空間
二次空間 二次空間
二次空間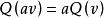 二次空間
二次空間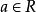 二次空間
二次空間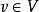 二次空間
二次空間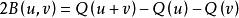 二次空間
二次空間 二次空間
二次空間映射被稱為在上的 二次形式,如果 對於所有 和 ,並且是在上的雙線性形式.
 二次空間
二次空間 二次空間
二次空間這裡的 被稱為 相伴雙線性形式;它是對稱雙線性形式。儘管這是非常一般性的定義,經常假定這個環 是一個域,它的特徵不是2。
 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間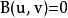 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間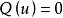 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間的兩個元素和被稱為 正交的,如果。雙線性形式的 核由正交於 V的所有元素組成,而二次形式 的 核由 的核中的有 的所有元素 組成。 如果2是可逆的,則 和它的相伴雙線性形式 有同樣的核。雙線性形式 被稱為 非奇異的,如果它的核是0;二次形式 Q被稱為 非奇異的,如果它的核是0。非奇異二次形式 的正交群是保持二次形式 的 V的自同構的群。
 二次空間
二次空間 二次空間
二次空間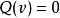 二次空間
二次空間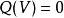 二次空間
二次空間 二次空間
二次空間二次形式 被稱為迷向的,如果有 中的非零的 v使得 。否則它稱為非迷向的。二次空間的一個向量或子空間也可以被稱為迷向的。如果 則 被稱為完全奇異的。
性質
二次空間的一些其他性質:
(1) Q服從平行四邊形定律:
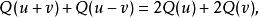 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間(2)向量和是關於正交的,若且唯若
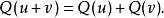 二次空間
二次空間實二次形式
 二次空間
二次空間假定是定義在實數向量空間上的二次形式。
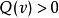 二次空間
二次空間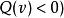 二次空間
二次空間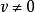 二次空間
二次空間1)被稱為是正定的(或者負定的),如果或者對於所有向量。
 二次空間
二次空間2)如果我們放鬆嚴格不等於為≥或≤,則形式被稱為半定的。
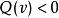 二次空間
二次空間 二次空間
二次空間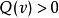 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間3)如果對於某個而且對於另一個,則被稱為不定的。
 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間設是如上那樣關聯於的實數對稱矩陣,所以對於任何列向量,由下式成立
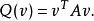 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間 二次空間
二次空間接著,是正(半)定的,負(半)定的,不定的,若且唯若矩陣有同樣的性質(參見正定矩陣)。最終,這些性質可以用的特徵值來刻畫。
