基本介紹
二次函式是最簡單的非線性函式,在最最佳化理論中具有重要的意義。根據函式的泰勒二次展開式,可以把一般的二次函式寫成以下向量形式:
 正定二次函式
正定二次函式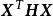 正定二次函式
正定二次函式式中, B為常數向量,相當於函式的梯度; H為n×n階常數矩陣,相當於函式的二階導數矩陣。 稱二次型, H稱二次型矩陣 。
矩陣有正定、負定和不定之分。對於任意非零向量 X:
 正定二次函式
正定二次函式(1) 若有 ,則稱矩陣且 H是正定矩陣。
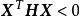 正定二次函式
正定二次函式(2)若有 ,則稱矩陣 H是負定矩陣。
 正定二次函式
正定二次函式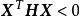 正定二次函式
正定二次函式(3)若有時 ,有時 ,則稱矩陣 H是不定矩陣。
由線性代數可知,矩陣 H的正定性除了可以用上面的定義判斷外,還可以用矩陣的各階主子式進行判別。所謂矩陣的主子式,就是包含第一個元素在內的左上角各階子矩陣所對應的行列式。
如果矩陣 H的各階主子式的值均大於零,即
一階主子式
 正定二次函式
正定二次函式二階主子式
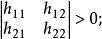 正定二次函式
正定二次函式三階主子式
 正定二次函式
正定二次函式 正定二次函式
正定二次函式則矩陣 H是正定的。
如果矩陣 H的各階主子式的值負正相間,即
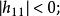 正定二次函式
正定二次函式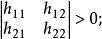 正定二次函式
正定二次函式 正定二次函式
正定二次函式 正定二次函式
正定二次函式即奇數階主子式小於零,偶數階主子式大於零時,矩陣 H負定,否則 H不定。
 正定二次函式
正定二次函式如果式(1)中的二次型矩陣 H是正定的,則稱函式 為 正定二次函式 。
性質介紹
在最最佳化理論中正定二次函式具有特殊的作用,這是因為許多最最佳化理論和最最佳化方法都是根據正定二次函式提出並加以證明的,而且所有對正定二次函式適用並有效的最最佳化算法,經證明,對一般非線性函式也是適用和有效的。
可以證明,正定二次函式具有以下性質:
(1)正定二次函式的等值線(面)是一族同心橢圓(球)。橢圓(球)族的中心就是該二次函式的極小點,如圖1所示。
(2)非正定二次函式在極小點附近的等值線(面)近似於橢圓(球),如圖2所示 。
 圖1 正定二元二次函式的等值線
圖1 正定二元二次函式的等值線 圖2 非正定二元二次函式的等值線
圖2 非正定二元二次函式的等值線
