簡介
引入
定型二次型是實二次型的類型。
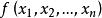 半正定二次型
半正定二次型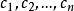 半正定二次型
半正定二次型設 是一個實二次型, 是任意 n 個不全為零的實數。實二次型分類如下:
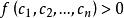 半正定二次型
半正定二次型1、若恆有,則 f 稱為正定的。
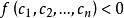 半正定二次型
半正定二次型2、若恆有,則 f 稱為負定的。
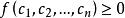 半正定二次型
半正定二次型3、若恆有,則 f 稱為半正定的。
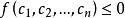 半正定二次型
半正定二次型4、若恆有,則 f 稱為半負定的。
5、其他情形的 f 稱為不定的。
定義
正定、半正定、負定、半負定的二次型合稱為定型二次型;不定的二次型稱為不定型二次型。
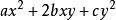 半正定二次型
半正定二次型高斯 (Gauss,C.F.) 在 1801 年出版的《算術的研究》中包含了對二次型的探討。他用行列式表示二次型 的判別式,還引進了正定、半正定、負定的概念。他引進的負定概念實際上是現在的半負定。
正定二次型
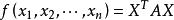 半正定二次型
半正定二次型 半正定二次型
半正定二次型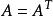 半正定二次型
半正定二次型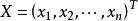 半正定二次型
半正定二次型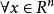 半正定二次型
半正定二次型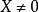 半正定二次型
半正定二次型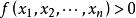 半正定二次型
半正定二次型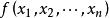 半正定二次型
半正定二次型 半正定二次型
半正定二次型設,其中矩陣是對稱陣,即,為列向量,若,,有,則稱為正定二次型,稱實對稱矩陣正定。
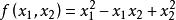 半正定二次型
半正定二次型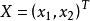 半正定二次型
半正定二次型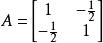 半正定二次型
半正定二次型例如,即為正定二次型,其中,。
