定義
 歐拉示性數
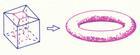
歐拉示性數假設g是曲面上洞眼的個數(比如球面沒有洞,故g=0;又如環面有一個洞,故g=1),那么e=2-2g。
g也是拓撲不變數,稱為曲面的虧格(genus)。
因此在平面上,e=2=p-l+n, 此即著名的歐拉公式。
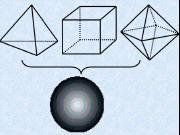
歐拉示性數 假設曲面上有一個三角剖分, 我們把所有三角形的頂點總個數記為p(公共頂點只看成一個,下同),邊數記為l,三角形的個數記為n,則e=p-l+n是曲面的拓撲不變數! 也就是說不管是什麼剖分, e總是得到相同的數值。 e被稱為稱為歐拉示性數。
 歐拉示性數
歐拉示性數稱為歐拉公式。V+F-E即歐拉示性數,已成為“拓撲學”的基礎概念。數論...的面數,E是多面體P的棱的條數,X(P)是多面體P的歐拉示性數。如果P可以...
歐拉其人 數論定理 幾何定理 拓撲公式 經濟學人物生平 萊昂哈德·歐拉 複平面上的Gamma 函式 歐拉1707年4月15日生於瑞士巴塞爾,1783年9月18日卒於俄國聖彼得...
人物生平 職業生涯 學術成就 主要成就 歐拉全集的面數,E是多面體P的棱的條數,X(P)是多面體P的歐拉示性數。如果P...)叫做P的歐拉示性數,是拓撲不變數,就是無論再怎么經過拓撲變形也不會改變...是多面體P的棱的條數,X(P)是多面體P的歐拉示性數。如果P可以同胚於一個...
基本介紹 公式介紹 平面幾何 拓撲學: 在歐拉公式中,令 f(p)=V+F-E,f(p)叫做歐拉示性數。定理告訴我們,簡單多面體的歐拉示性數f (p)=2。 除簡單多面體外,還有...的歐拉示性數為f (p)=16+16-32=0, 所以帶一個洞的多面體...
歐拉定理 定理的證明 定理的意義 歐拉定理又一證法人物生平 萊昂哈德·歐拉 複平面上的Gamma 函式 歐拉1707年4月15日生於瑞士巴塞爾,1783年9月18日卒於俄國聖彼得...
人物生平 職業生涯 學術成就 主要成就 歐拉全集),可以找到歐拉示性數與貝蒂數之間的關係式: 其中αi為復形K的i維單形個數,b)i為多面體│K│的i維貝蒂數,(K)即K的歐拉示性數。從而證明了歐拉示性數是│K│的拓撲不變數。 單純復形的整係數同調群是個有限生成...
同調論 正文 配圖 相關連線體積和歐拉示性數就是兩個重要的不變數。 研究的問題 在坐標平面上,考慮任何...恰好等於x,歐拉示性數恰好等於y? 這就是曲面地理學所要研究的問題...
曲面地理學 研究的問題:典範體積 K_X^2(也就是典範除子的自 相交數),上同調的 歐拉示性數 χ(O_X), 拓撲的歐拉示性數χ_{top}(X)。 不變數是反映...
定義 不變數 地理學問題 性質 例子