霍奇理論
正文
關於調和微分形式的理論。19世紀德國數學家（G.F.）B.黎曼利用狄利克雷原理，將單復變數的代數函式及其積分，和一系列函式類的存在，建立在黎曼曲面的拓撲和勢的構造上。這門學問推廣到高維流形時，霍奇理論進一步揭示了分析與拓撲之間的深刻聯繫，給當代流形上分析的整體研究以巨大影響。這個理論為英國數學家W.V.D.霍奇首創於30年代，而後為小平邦彥等數學家大大發展與套用。
設M為n維黎曼流形,在局部坐標系(x1,x2,…,xn)中，黎曼度量表示成
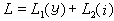。記矩陣G =(gij),G-1=(gjk),g =detG。M上的任一r階C∞微分形式φ在該坐標系中可表示成φ=
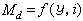其中係數
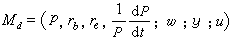均是C∞函式且關於下指標反對稱。M上的這種r階形式全體記為Er。設ψ∈Er,令 
，
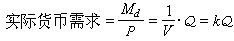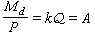
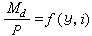
在Er上定義外微分運算元d如下:對於函式ƒ∈E0,dƒ=
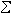
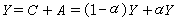；對於
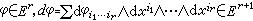。 令δ: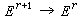
為d關於上述內積的形式共軛運算元，即對於ω∈Er+1,在φ,ω 二者之一有緊支集時成立(dφ,ω)＝ (φ,δω)。定義 Δ: Er→Er為
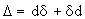，稱它是M上的拉普拉斯-貝爾特拉米運算元。在M是歐氏空間，r=0的情形，Δ即為普通的拉普拉斯運算元。 利用線性運算元*:Er→Enn-r(*運算元或霍奇運算元)可將δ,從而Δ明確地局部表示出來。運算元*滿足條件
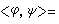
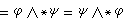。在局部坐標系中,它可寫成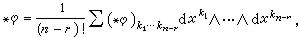 
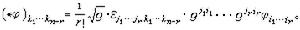
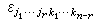是指標(j1…jrk1…kn-r)的置換符號，
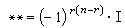,這裡I為恆同運算元,(*φ,*ψ)=(φ,ψ)。利用這些性質可以推出
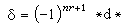。上述這些運算元尚有下列關係：
，
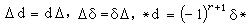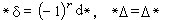。 滿足方程dφ=0的φ稱為閉微分形式。若存在α,使φ＝dα, 則φ稱為正合微分形式。由於d2=0,正合形式必是閉的。若dφ=0,δφ=0同時成立，稱φ為調和微分形式。德·拉姆定理指出,德·拉姆上同調群{閉的r階C∞微分形式}/{正合的r階C∞微分形式}與實係數的r 階奇異上同調群同構，而霍奇理論即要表明在每個上同調類中是否存在調和的微分形式。
緊黎曼流形 設M是緊的黎曼流形，則Δφ=0意味著φ調和，因為(Δφ，φ)＝(dφ，dφ)+(δφ，δφ)，從而dφ=0,δφ＝0。記lr為Er按上述範數完備化的希爾伯特空間,那么d,δ,Δ均可擴充定義到整個lr上。這時δ為d的共軛運算元，Δ為自共軛的橢圓型運算元。對於Δφ＝α的任一弱解φ，在α是C∞微分形式時,φ也是C∞的。因此任一調和微分形式均是C∞光滑的。以Hr記M的 r階調和微分形式全體，P:lr→Hr為射影運算元,那么霍奇理論的中心結果為下述分解：
①lr=Δ(lr)
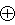Hr=d(lr_1)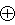δ(lr+1)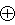Hr。 易知對任一α∈Δ(lr),Δφ =α在Δ(lr)中的解惟一。
② 存在格林運算元G:lr→Δ(lr)，Gα=φ，對β∈Hr,Gβ=0。
由定義，GP=PG=0, P+ΔG =I，Gd=dG，Gδ=δG，於是對每個φ∈lr,dφ =0者, 由①得φ=dδGφ +Pφ。它表明調和形式Pφ與φ在同一個德·拉姆上同調類內,且是這個類中惟一的調和形式。
③ 實係數的r階奇異上同調群與 r階調和形式空間Hr同構。
④ Hr為有限維向量空間。若記hr=dimHr,ⅹ(M)為M的歐拉示性數，則ⅹ(M)=∑(-1)rhr。
如果考慮帶有某種奇性的微分形式所構成的希爾伯特空間時，就得到黎曼曲面上第二、三類阿貝爾微分的推廣。
全純向量叢 設π：E →M是秩為l的全純向量叢。M是緊的復m 維埃爾米特流形。令A(p,q)(E)為係數在E 中的C∞(p，q)形式全體。{Tjk}是定義在M的坐標覆蓋{Uj}上能確定E的轉移函式矩陣。這時 φ∈A(p,q)(E)在Uj上表示成
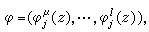這裡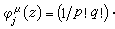
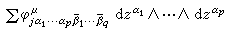
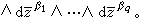在Uj ∩Uk上成立 
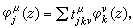這裡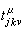 
是矩陣Tjk的元素，均是全純函式。定義
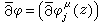。因為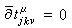
，所以這個定義不依賴局部坐標的選取。 E 的纖維上的埃爾米特形式是由每個Uj上給出一個正定形式
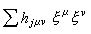確定的。以hj記矩陣(
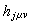),那么應滿足條件
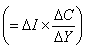。設M上的埃爾米特度量在Uj上表示為
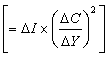,在A(p,q)(E)內引入內積如下：對於φ,ψ∈Ap,q(E)，記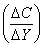
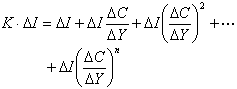。這裡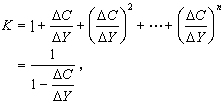
然後內積與範數分別為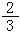
令
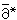為扺關於上述內積的共軛運算元,作
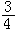E值(p，q)形式φ稱為扺閉的,如果扺φ=0,稱為扺 正合。如果存在α∈Ap,q_1(E)使φ=扺α,且□φ=0,稱φ為調和的E值(p,q)形式。它等價於扺φ=0, 扺*φ=0同時成立,記其全體為Hp,q。令lp,q為Ap,q(E)按上述範數的完備化，它到Hp,q的正交射影仍記為P，那么成立：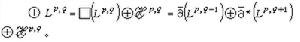
② 存在格林運算元G:lp,q→□(lp,q),在□(lp,q)上一一。Gφ=0，φ∈Hp,q。□G+P=I。
③ 若φ為閉形式,則Pφ與φ在同一個多博爾特上同調類即
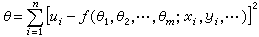/{扺-正合的E值(p,q)形式}。 ④Hp,q為有限維向量空間。
凱勒流形 設M為緊的凱勒流形，它的凱勒度量為
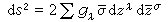。將它看做M上的埃爾米特度量，考慮M上的平凡線叢E=M×C及C上的歐氏度量。按上面的構造方法有對應的運算元□。另一方面
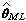作為M上的黎曼度量有對應的運算元Δ 。在凱勒條件下成立Δ=2□。因此除了前面的一些結論外，尚有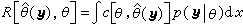 
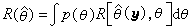，則x(M)=
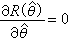。一個簡單的推論即為凱勒流形的第奇數個貝蒂數為偶數。 當M是非緊流形時，對於不同的微分形式所構成的希爾伯特空間有相應的空間分解。當M為某個流形上有邊界的區域時，將導致各類紐曼問題。特別地, 當M是複流形中有光滑邊界的區域時，產生著名的扺-紐曼問題，它對於多複變函數論、超定微分方程組、擬微分運算元等學科的發展起了重大作用（見多複變函數論）。
由霍奇理論可知底流形的拓撲影響著調和形式的存在與否，存在多少；反過來，由流形的度量往往能夠知道調和形式的存在與否，從而產生了許多上同調群的消隱定理。
參考書目
W.V.D.Hodge,The Theory and Applications of harmonic Integrals,2nd ed., Cambridge Univ.Press, Cambridge, 1952.
K.Kodaira,Harmonic Fields in Riemannian Manifolds,Ann. of Math.,50, pp. 587～665, 1949.
K.Kodaira,On a Differential-Geometric Method in the Theory of Analytic Stacks,Proc. nat.Acad. Sci. U. S. A.,39, pp. 1268～1273, 1953.
J.J.Kohn,Harmonic Integrals on Strongly Pseudoconvex Manifolds, I,Ann. of Math.,78, pp. 112～148, 1963;Ⅱ,ibid,79, pp. 450～472, 1964.
S.Nakano,On Complex Analytic Vector Bundles,J. Math. Soc.Japan 7, pp. 1～12, 1955.
