概述
極小化極大問題的定量研究起源於上個世紀的七十年代,主要研究其解的存在性及求解方法。極小化極大問題是一類非常重要的數學規劃問題,其求精確求解非常重要,通常通過各式各樣的疊代算法 。在工程設計、決策理論、自動控制、經濟管理、統計學、哲學等領域都有著十分廣泛的套用。
概念
極小化極大問題歸結如下:
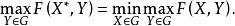 極小化極大
極小化極大 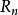 極小化極大
極小化極大 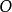 極小化極大
極小化極大 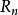 極小化極大
極小化極大  極小化極大
極小化極大 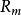 極小化極大
極小化極大 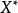 極小化極大
極小化極大 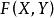 極小化極大
極小化極大 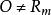 極小化極大
極小化極大 是n維實數空間,其中 是 的一個閉凸子集, 是 的一個有界閉子集,求解 ,如果 是線性的,則丄式就是極小化極大問題。如果 ,則上式表示有約束的極小化極大問題。
目標函式對於極小化極大問題,雖然目標函式有時是可微的,但其極大值函式通常不可微。因而極小化極大問題是不可微最佳化問題。
分類
從模型角度,極小化極大問題可以分為兩類:
離散的極小化極大問題
離散的極小化極大問題表示為:
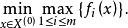 極小化極大
極小化極大 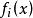 極小化極大
極小化極大 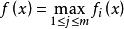 極小化極大
極小化極大 其中, 為目標函式, 成為極大值函式。
連續的極小化極大問題
連續的極小化極大問題表示為:
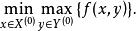 極小化極大
極小化極大 對於以上兩類問題,又可各自分為有約束的極小化極大問題和無約束的極小化極大問題。
求解方法
對於極小化極大問題,主要有三種基本思路。
 極小化極大
極小化極大 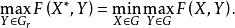 極小化極大
極小化極大 (1)找出極值集合 ,使得
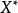 極小化極大
極小化極大  極小化極大
極小化極大  極小化極大
極小化極大 要求解 使得極大值函式最小,必須要先找出使得目標函式極大的極值集合 ,繼而就可以在 求得極大值函式的極小值。
 極小化極大
極小化極大 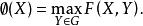 極小化極大
極小化極大 (2)求極大值函式 的最小:
要求解極小化極大問題,可以通過缺點極大值函式,研究極大值函式的性質求得其最小值點。
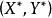 極小化極大
極小化極大 (3)找打一個鞍點 ,使得:
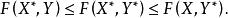 極小化極大
極小化極大 即通過求解鞍點來求解極小化極大值最佳化問題 。
