定義
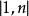 有限集合
有限集合定義1 小於或等於某一自然數n的那些自然數的集合叫做 自然數串的 一個線段,並用符號 來表示。
定義2 與自然數串的一個線段對等的集合,以及空集合,都叫做 有限集合;不是有限集合的集合叫做 無限集合。
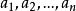 有限集合
有限集合換句話說,有限集合(如果它不是空的)就是這樣的集合,它的元素是可以“編號”的,也就是,可以把它的元素編上號碼,寫成: ,並且所有的元素都已數到,從1到n的各個自然數全被用過而且不同的元素得到了不同的號碼,至於無限集合則是它的元素不能被這樣“編號”的集合,與有限(或無限)集合等勢的集合是有限的(相應地,是無限的),介紹有限集合和無線集合的另一種定義。
定義3 不含有與其自身對等的真子集合的集合,以及空集合,都叫做 有限 集合,不是有限集合的集合叫做 無限集合。
從下面定理1和定理7就推出:定義2與定義3是等價的,事實上,如果集合在定義2的意義下是有限的,那么,根據定理1,它在定義3的意義下也是有限的,反過來,如果集合在定義3的意義下是有限的,那么,在定義2的意義下它應該也是有限的,因為,如若不然,它在定義2的意義下是無限的,從而根據定理7,它在定義3的意義下也是無限的,而這是不可能的,因此,有限集合的兩個定義是等價的,由此(利用反證法)立刻推出無限集合的兩個定義的等價性。
我們要指出,定義3要比定義2好一些(誠然,這只是在形式上如此),因為它是用集合的一般理論的術語陳述出來的,而定義2卻是以自然數串的一些熟知的性質為其先決條件的。
相關性質定理
定理1
(有限集合的基本定理)有限集合不能與它的任何真子集合或真母集合對等。
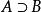 有限集合
有限集合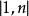 有限集合
有限集合 有限集合
有限集合證明: (文中所有定理的詳細證明請參考文後書籍)定理中兩個論斷(與子集合和母集合的不對等)的每一個論斷,都可以容易地從另一個論斷推出,因為,如果A~B而且,那么從A和B兩集合之一的有限性,像上面已經指出的那樣,即可推出另一集合也是有限的.因此,例如.讓我們來證明:有限集合小能與它的真子集合對等,對於空集A=0,定理是成立的,因為空集合絕不會有真子集合,設A≠0,於是,按照有限集合的定義,集合A便對等於自然數串的一個(至少對等於一個)線段,現在讓我們對於數n用歸納法證明:A不可能一一映象在它自己的真子集合B上,對於n=1,這是顯然的,因為而且只包含一個元素,B=0是它唯一的一個真子集合,所以A不對等於B。
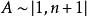 有限集合
有限集合假設定理對於自然數n已被證明了,我們要證明定理對於n+1也是正確的,因此,設,而且f是A 在B上的一個一一映象,用與A的元素對應的那些自然數給A的元素編號,我們將得到
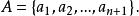 有限集合
有限集合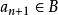 有限集合
有限集合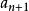 有限集合
有限集合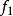 有限集合
有限集合 有限集合
有限集合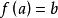 有限集合
有限集合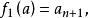 有限集合
有限集合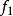 有限集合
有限集合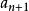 有限集合
有限集合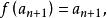 有限集合
有限集合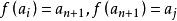 有限集合
有限集合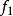 有限集合
有限集合 有限集合
有限集合 有限集合
有限集合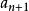 有限集合
有限集合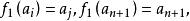 有限集合
有限集合 有限集合
有限集合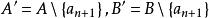 有限集合
有限集合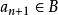 有限集合
有限集合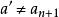 有限集合
有限集合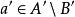 有限集合
有限集合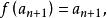 有限集合
有限集合 有限集合
有限集合 有限集合
有限集合對於B=0,論斷是正確的,如果B≠0.那么,無損於普遍性。可設,因為如若不然,我們取b∈B,並在B中用代換b而造成新集合B;再構成新映象,使它和映象,除了具有性質的元素a之外,對於A的其他所有元素完全相同,並且假定對於元素a有於是就是A在其含有的真子集合B上的一個一一映象。其次,無損於普遍性,可以認為因為如若不然。設,於是,再構成新映象,使它和映象,除了和這兩個元素外,對於A的其他所有元素完全相同;並且假定因此,總起來,我們設並更設,因為B是A的真子集合,所以有元素a'∈A\B.因為,所以,因而,這就是說,B'是A'的一個真子集合。因為所以映照便建立起了集合A'與B'的對等性,但是所以我們便得到了與歸納法假定相矛盾的結果,而我們定理的淪斷正就是那個假定,因此,這就是說,全部定理已被證明。
從定理1容易推出定理2。
定理2
每一個非空有限集合與自然數串的一個線段而且僅只一個線段對等。
定義4
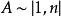 有限集合
有限集合對於非空有限集合A,由所唯一確定的自然數n叫做集合A的元素數,數0叫做空集合的元素數。
從對等的性質就推出:兩個有限集合在而且僅只在它們具有相同的元素數時,才是對等的,所以,可以把元素數看成是有限集合的勢的定義。
定理3
有限集合的任一子集合是有限集合,無限集合的任一母集合是無限集合。
定理4
有限集合A的元素數永遠大於它的真子集合B的元素數。
定理5
全部自然數組成的集合N,以及含有與N對等的子集合的集合,全是無限集合。
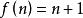 有限集合
有限集合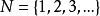 有限集合
有限集合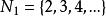 有限集合
有限集合證明: 集合N是無限的,因為對於任一自然數n的映象,把集合一一地映象在它的真子集合上,這就是說,任一與N對等的集合N‘’是無限的,而按照定理3,於是,包含與N對等的集合N'作為其子集合的任一集合,也是無限的。
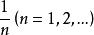 有限集合
有限集合例 實數集合或複數集合包含自然數集合N,因此,它們都是無限集合,線段[0,1]也是無限集合,因為它含有與N對等的形如那樣的數組成的集合N。
定義5
對等於自然數集合的集合,叫做 可排集合。
換句話說,可排集合就是這樣的集合:可以利用自然數把它的元素如此地“編號”,使得全部自然數全被用到而且不同的元素水遠有不同的號碼,因此,可排集合A永遠可被寫成這樣的形狀:
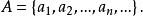 有限集合
有限集合偶數集合或奇數集合,以及有理數集合,全都是可排集合。
定義5
不是有限的或是可排的集合,叫做不可排集合。
定理6
每一個無限集合必含有一個可排集合。
定理7
每一個無限集合M必與其某一個真子集合對等。

