定義
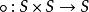 半群
半群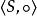 半群
半群 半群
半群非空集合S,S上定義了二元運算 ( 稱為廣群)。若運算 滿足結合律,即:
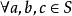 半群
半群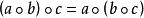 半群
半群,有
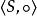 半群
半群則稱 為 半群。
意義
半群是最簡單、最自然的一類代數系統。一個非空集合S連同定義在它上面的一個結合的(即滿足結合律的)二元運算“·”的代數系統(S,·)稱為一個半群.半群(S,·)簡記為S。
半群是群的推廣。群自然是半群;反之顯然未必。半群也是環的推廣。環在只考慮它的乘法運算的時候是一個半群,稱為環的乘半群;但任何一個帶零半群卻未必是某個環的乘半群。半群代數理論的系統研究始於20世紀50年代(雖然,這方面的工作可追溯到1904年蘇士凱維奇(Suschkwitz,A.K.)關於有限半群的論文)。在數學內部和外部的巨大推動下,半群理論已成為代數學的一個公認的分支學科,並早已以其特有的方法獨立於群論和環論之外。在20世紀60年代,蘇聯和美國率先出版了兩本專著,利雅平(Ляпин,E.C.)的《半群》和克利福德(Clifford,A.H.)與普雷斯頓(Preston,G.B.)的兩卷《半群代數理論》,這對半群代數理論的發展,在國際上起了巨大的推動作用。由德國斯普林格出版社出版的《半群論壇》更是有關半群理論的一個重要的國際性專門刊物.許多數學家在世界各地開展半群理論的研究和各層次高級人才的培養(直到博士後)。半群代數理論是半群理論中最基本、最活躍、也最富成果的一部分。此外,尚有半群的分析、拓撲和序理論。
群
群是一種只有一個運算的、比較簡單的代數結構;是可用來建立許多其他代數系統的一種基本結構。
設G為一個非空集合,a、b、c為它的任意元素。如果對G所定義的一種代數運算“·”(稱為“乘法”,運算結果稱為“乘積”)滿足:
(1)封閉性,a·b∈G;
(2)結合律,即(a·b)c = a·(b·c);
(3)對G中任意元素a、b,在G中存在惟一的元素x,y,使得a·x= b,y·a=b,則稱G對於所定義的運算“·”構成一個群。例如,所有不等於零的實數,關於通常的乘法構成一個群;時針轉動(關於模12加法),構成一個群。
滿足交換律的群,稱為交換群。
群是數學最重要的概念之一,已滲透到現代數學的所有分支及其他學科中。凡是涉及對稱,就存在群。例如,可以用研究圖形在變換群下保持不變的性質,來定義各種幾何學,即利用變換群對幾何學進行分類。可以說,不了解群,就不可能理解現代數學。
1770年,拉格朗日在討論代數方程根之間的置換時,首先引入群的概念,而它的名稱,是伽羅華在1830年首先提出的。
環
對並與差運算封閉的集類,測度論中重要概念之一。設F是Ω上的一個非空集類。如果它對集的並及差運算封閉,即對任何A,B∈F,都有A∪B∈F,A\B∈F,則稱F為Ω上的環。例如,若F是由實直線R上任意有限個左開右閉的有限區間的並集:
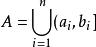 半群
半群的全體構成的集類,則F是R上的一個環。環也是對於交與對稱差運算封閉的集類,並按這兩種運算成為布爾環(參見第一卷《布爾代數》).要把R上的勒貝格測度和勒貝格-斯蒂爾傑斯測度以及相應的積分理論推廣到更一般的集合上,就需要做一系列奠基工作,其中之一是建立一些特殊的集類並研究其性質。環以及半環、σ環、代數、σ代數等重要集類正是為了這一目的而引入的。
推廣概念
有限半群
有限半群是與群論中有限群相平行的概念。半群S稱為有限的,若|S|<∞。艾倫伯格(Eilenberg,S.)的《自動機,語言與機器》的卷B實際上是有限半群論。有限變換半群、有限半群的分解和分類等構成有限半群理論的重要課題。
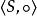 半群
半群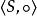 半群
半群設 是半群,若S是有限集,則稱 是 有限半群。
子半群
子半群是與群的子群相平行的概念。設S是一半群,≠US,若關於任意u,v∈U,有uv∈U,則稱U是S的子半群。用U≤S表示U是S的子半群。
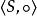 半群
半群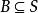 半群
半群 半群
半群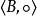 半群
半群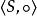 半群
半群設 是半群, , 在B上封閉,則容易驗證 也是半群,稱為 的 子半群。
么半群
么半群是指含麼元(即恆等元)的半群。半群M,若存在1∈M,使得關於任意x∈M,有x1=1x=x,則稱M為么半群.關於任意半群S,常用S表示一個么半群.若S為么半群,則S1=S;若S不是么半群,則S1=S∪{1},1S,S1的半群運算定義如下:在S上其運算與S的半群運算相同,而關於任意x∈S有x1=1x=x,且1·1=1。
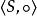 半群
半群設 是半群,若S中存在單位元(麼元),即:
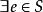 半群
半群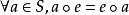 半群
半群,使 。
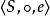 半群
半群則稱 為 么半群。
交換半群
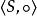 半群
半群 半群
半群設 是半群,若運算 滿足交換律,即:
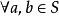 半群
半群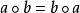 半群
半群,有 。
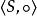 半群
半群則稱 是 交換半群。

