基本介紹
 有理點
有理點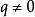 有理點
有理點實數由有理數與無理數兩部分組成,有理數包括零、正負整數和正負分數。 有理數可寫成 的形式(其中p、q為整數,且 ),也可表示為整數、有限小數或無限循環小數,而 無理數只能表示成無限不循環小數。
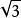 有理點
有理點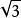 有理點
有理點實數與數軸上的點是一一對應的.為了簡便起見,我們常用同一個字母或數字既表示某個實數又表示以此實數為坐標的數軸上的對應點,比如,數a與點a,數 與點 ,……
數軸上表示有理數的點稱為 有理點,表示無理數的點稱為 無理點。
有理點的稠密性
有理點具有稠密性,即數軸上任意兩個不同的有理點之間一定存在無窮多個有理點;同樣地,無理點也具有稠密性。有理數經過四則運算(除數不為零)其結果仍為有理數;而無理數經過四則運算其結果可能為無理數也可能為有理數。
設有一條水平直線,在這條直線上取定一點 O,稱為原點,規定一個正方向(習慣上規定由原點向右的方向為正方向),再規定一個長度,稱為單位長度,這種具有原點、正方向和單位長度的直線稱為 數軸。
 有理點
有理點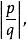 有理點
有理點 有理點
有理點 有理點
有理點任何一個有理數 ,都可以在數軸上找到一個點與之對應,使得由原點到這點的長度與單位長度之比等於 這樣得到的點稱為 有理點,它是有理數 的幾何表示,而 稱為有理點的坐標,反之,數軸上任何一個有理點必對應於一個有理數。
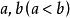 有理點
有理點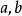 有理點
有理點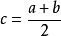 有理點
有理點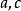 有理點
有理點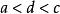 有理點
有理點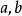 有理點
有理點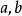 有理點
有理點任給兩個有理數 ,在 之間至少可以找到一個有理數c,使得a<c<b,例如 ,同樣地,在 之間也至少可以找到一個有理數d使 ,以此類推,可知不論有理數 相差多么小,在 之間總可以找到無窮多個有理數,這就是 有理數的稠密性,因為任何一個有理數必和數軸上的一個有理點相對應,因此數軸上任意兩個有理點之間總可找到無窮多個有理點,即有理點在數軸上是稠密的。
 有理點
有理點 有理點
有理點 有理點
有理點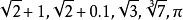 有理點
有理點雖然有理點在數軸上處處稠密,但是有理點尚未充滿數軸。例如邊長為一個長度單位的正方形,其對角線的長度為 個長度單位,可以證明 不是有理數,因此數軸上坐標為 的點不是有理點,這種點也有無窮多個,而且在數軸上也是處處稠密的。例如,坐標為 等的點都不是有理點,因此,數軸上除有理點之外還有無窮多個“空隙”,這些空隙處的點稱為 無理點,與無理點相對應的數稱為無理數。
相關知識
 有理點
有理點 有理點
有理點 有理點
有理點 有理點
有理點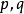 有理點
有理點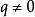 有理點
有理點人們對數的認識是逐步發展的,先是自然數,繼而發展到有理數(即正負整數、正負分數及0),再進一步就發展到無理數(例如 、 等都是無理數). 有理數可以表示為 , 無理數不能表示為 ,其中 都是整數,且。
分數可以用有窮小數或無窮循環小數表示,反之,有窮小數或無窮循環小數亦可用分數表示。
因此,有理數可以表示為有窮小數或無窮循環小數,而無理數為無窮不循環小數。
有理數與無理數統稱為 實數,實數充滿數軸而且沒有空隙,這就是實數的連續性,由此可知,每一個實數必是數軸上某一個點的坐標;反之,數軸上每一點的坐標必是一個實數,這就是說全體實數與數軸上的全體點形成一一對應的關係,一般我們所研究的數都是實數,為了簡單起見,常常將實數和數軸上與它對應的點不加區別,用相同的符號表示,如點a和實數a是相同的意思。
在平面直角坐標系中,橫、縱坐標都是整數的點叫 格點,格點又稱為整點;橫、縱坐標都是有理數的點稱為 有理點,格點是有理點,不是有理點的點稱為無理點。
直角坐標平面上頂點均為有理點的三角形稱為 有理點三角形,頂點均為格點的三角形稱為 格點三角形(或整點三角形),類似地,頂點均為有理點的n(n>3)邊形稱為 有理點n邊形;頂點均為格點的n邊形稱為 格點n邊形(或 整點n邊形)。
有理點性質
性質1
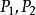 有理點
有理點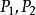 有理點
有理點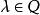 有理點
有理點設 是有理點,P是 的定比分點,若定比 ,則P點必為有理點。
特別地,兩個有理點的中點是有理點。
性質2
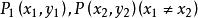 有理點
有理點過兩個有理點 的直線斜率是有理數。
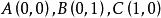 有理點
有理點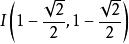 有理點
有理點利用性質1、性質2易得:有理點三角形(見“相關知識”)的重心、外心、垂心均為有理點,而它的內心未必是有理點。例如:頂點坐標為 的三角形ABC的內心坐標為 ,是個無理點。
性質3
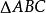 有理點
有理點若 是有理點三角形,則只要tanA、tanB、tanC有意義,它們就均為有理數。
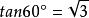 有理點
有理點由 是無理數知有理點三角形不可能是正三角形,特別地,格點三角形不可能是正三角形。
判別有理點和無理點
 有理點
有理點 有理點
有理點 有理點
有理點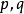 有理點
有理點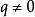 有理點
有理點有理數可以表示為 ,即 有理數可寫成 的形式, 無理數不能表示為,其中 都是整數,且。
分數可以用有窮小數或無窮循環小數表示;反之,有窮小數或無窮循環小數亦可用分數表示。因此, 有理數也可表示為整數、有限小數或無限循環小數,而 無理數只能表示成無限不循環小數。
 有理點
有理點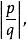 有理點
有理點 有理點
有理點 有理點
有理點任何一個有理數 ,都可以在數軸上找到一個點與之對應,使得由原點到這點的長度與單位長度之比等於 這樣得到的點稱為 有理點,它是有理數 的幾何表示,而 稱為有理點的坐標,反之,數軸上任何一個有理點必對應於一個有理數。

