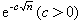有理函式逼近
以後，С.Η.伯恩斯坦、A.И.阿希耶澤爾及E.И.佐洛塔廖夫等套用切比雪夫理論解決了一系列具體函式用有理函式的最佳逼近問題。特別是左洛塔廖夫研究了在二個不同區間上具體函式的有理函式最佳逼近問題，這在濾波理論上有重要的套用。以後，在Α.Η.柯爾莫哥洛夫和C.H.梅爾捷良等影響下，A.A.貢恰爾、Ε.∏.多爾任科、A.∏.布拉諾夫、∏.∏.彼得魯曉夫等作了很多深刻的研究。特別地，在50年代開始，他們對逼近的反問題，即從有理函式最佳逼近值趨向於零的速度來研究逼近函式的結構性質方面作了一系列的研究。以後在正問題上，即從函式的結構性質來研究有理函式最佳逼近階的估計以及在研究有理函式最佳逼近值與多項式逼近值之間的關係與差別方面也得到了不少重要的結果。應該指出，在正問題方面，D.J.紐曼在1964年跨出了關鍵性的一步，他指出對│x│用n次有理函式逼近得到的階的估計為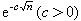
,大大地超過用n次多項式逼近的階
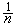。以後，匈牙利學者P.圖蘭、G.弗洛伊德等也作出了很多重要的研究。 設【α,b】為實軸上的閉區間（有窮或無窮），ƒ(x)是【α,b】上的實值連續函式，令
,
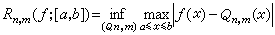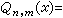
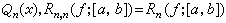, 稱它為ƒ(x)在【α,b】上用n次有理函式逼近時的最佳逼近值。若m＝0，Qn(x)就是 n次多項式,此時將Rn(ƒ;【α,b】)記作En(ƒ;【α,b)】)，稱它為ƒ(x)在【α,b】上用n次多項式Qn(x)逼近時的最佳逼近值。 1964年紐曼所得到的結果為：
，
，
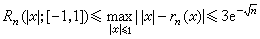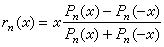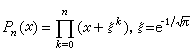且對於任意的偶有理函式Qn(x),有
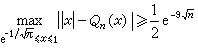。由此看出,用n次有理函式逼近│x│時，逼近的階比用n次多項式逼近時好得多。 圖蘭在1966年指出,有理函式rn(x)的極點對稱地分布在虛軸上,記作iyn,則
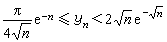, 它很快地趨向於原點。正是由於這個原因,儘管函式│x│在x=0處的性質不太好,但是由於這裡所取的有理函式的極點的極限點正是x=0這一點,因此在某種意義下消除了其“奇性”，得到了較好的結果。 紐曼還對一般的函式類套用他的方法及結果，得到有理函式逼近階的估計。後來，貢恰爾、布拉諾夫、∏.∏.維亞切斯拉沃夫等先後對紐曼結果作出了進一步的改進。此外，也對其他特殊函式研究有理函式最佳逼近值的上、下界估計。
對於其他一般的函式類也有很多研究，如彼得魯曉夫得到下列二個重要的結果：
① 設ƒ(l)(x)是【0,1】上的凸函式，則
；
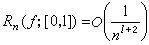此外，還有不少研究解析函式的有理函式最佳逼近問題的工作。例如,1978年B.H.羅薩克得到一個結果。設函式ƒ(z)在|z|<1解析,在|z|≤1上連續且在|z|=1上分段(共有m段)解析，則可以找到具有極點在│z│>1中的n次有理函式Qn(z),使
。若ƒ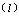
(z)具有有界變差，則有 
。
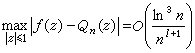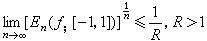，則ƒ(x)可以從【-1,1】解析開拓到以±1為焦點，長短半軸之和為R的橢圓中去。但是對於有理函式逼近,情況可以完全不同,不管Rn(ƒ;【-1,1】)以多么快的速度趨向於零，仍然不能保證ƒ(x)在【-1,1】上有很好的結構性質，更談不上具有解析性質了。必須除去一個例外集，ƒ(x)才有較好的結構性質。有人還將這些結果推廣到複數域中去。 如果想要從有理函式逼近的速度來推出函式在整個逼近的區間上被逼近函式的性質，就還需要給出有理函式極點分布的情況。這實際上也與給定極點有理函式逼近的逆定理有關了。
