簡介
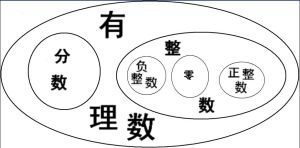 包含關係圖
包含關係圖正有理數:即有理數中的一個小部分。
有理數的含義是:能精確地表示為兩個整數之比的數。
有理數按性質分為正有理數、0、負有理數。
包含
正有理數還被分為正整數和正分數,包括等數。無限循環小數是有理數。
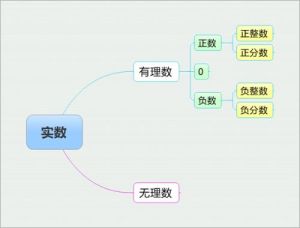
正有理數,數字名詞之一。所有大於0的有理數叫正有理數。
 包含關係圖
包含關係圖正有理數:即有理數中的一個小部分。
有理數的含義是:能精確地表示為兩個整數之比的數。
有理數按性質分為正有理數、0、負有理數。
正有理數還被分為正整數和正分數,包括等數。無限循環小數是有理數。
將一個或多個有理數的值相加的過程叫有理數的加法,如:23+64+52=139。
分析理解 有理數加法 加法解析 例子有理數,是整數和分數的統稱,一切有理數都可以化成分數的形式。注意:有理數集可用大寫黑正體符號Q代表。但Q絕對不表示有理數。因為有理數集與有理數是兩個不同...
基本概況 基本含義 包括內容 運算定律 產生法則一、除以一個不等於0的數等於乘以這個數的倒數。(注意:0沒有倒數)公式:a÷b=a×1/b 法則二、兩數相除,同號得正,異號得負,並把絕對值相除。(...
有理數除法法則 說明圖"乘方運算的結果叫冪(power)。 umber)
證明:假設√2不是無理數,而是有理數。 √2=p/q 由於2q^2是偶數,p
(1)兩數相乘,同號為正,異號為負,並把絕對值相乘。 (3)幾個不等於0的數字相乘,積的符號由負因數的個數決定。 (4)幾個數相乘,有一個因數為0時,積為0.
(3)幾個不等於0的數字相乘,積的符號由負因數的個數決定。 (4)幾個數相乘,有一個因數為0時,積為0.有理數(ration 整數和分數統稱為有理數,任...
數學術語 有理數"所有的有理數都可以表達成分數的形式. 在有理數的集合中
