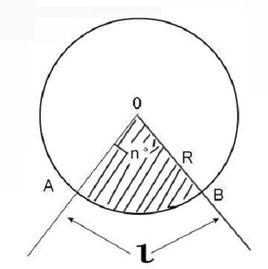
公式
 扇形面積公式
扇形面積公式 扇形面積公式
扇形面積公式 扇形面積公式
扇形面積公式設一扇形的半徑為 ,弧長為 ,面積為 ,則
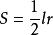 扇形面積公式
扇形面積公式 扇形面積公式
扇形面積公式若命扇形的頂角(扇形的弧所對的圓心角,叫做扇形的頂角)為 ,那么
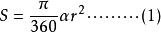 扇形面積公式
扇形面積公式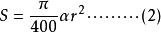 扇形面積公式
扇形面積公式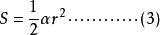 扇形面積公式
扇形面積公式其中(1)式適用於六十分制,(2)式適用於百分制,(3)式適用於徑制(弧度制)。
推導過程
提要。由定理“等半徑的兩個扇形的面積之比等於它們的弧長之比”,將圓看作扇形,利用弧長公式和圓的面積公式即可。
注意事項
•扇形還與三角形有相似之處,上述簡化的面積公式亦可看成:弧長與半徑乘積的一半,與三角形面積,為底和高乘積的一半相似。