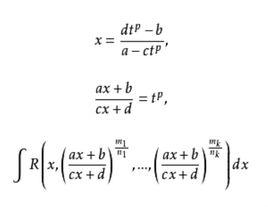有理代換

有理代換是求積分時常用的一種代換，用有理函式作的變數代換。當被積函式中含有x的根式時，一般可做代換去掉根式，從而求得積分，也就是說在積分法中，有理代換主要用於含有根式的積分，使被積函式有理化後再求原函式。

基本介紹

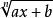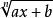有理代換

有理代換

當被積函式中含有x的一次根式 時，一般可作代換t= 來去掉根式，從而求得積分，這種代換稱為有理代換，有理代換的原則是“見根號，去根號”。

設R是k+1元有理函式，a，b，c，d是實數，m，m，…，m是整數，p是正整數n，n，…，n的最低公倍數。有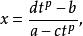理代換

有理代換

即

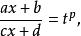有理代換

可把積分

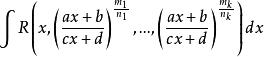有理代換

化為關於t的有理函式的積分 。

例題解析

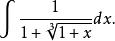有理代換

【例1】求

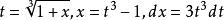有理代換

解：令 得

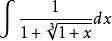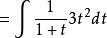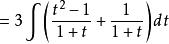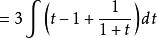有理代換

有理代換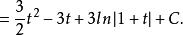

有理代換

有理代換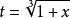

有理代換

有理代換

將代入上式得：

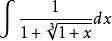有理代換

有理代換

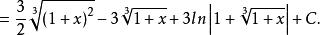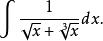有理代換

【例2】求

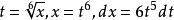有理代換

解：令，得：

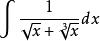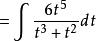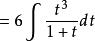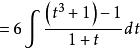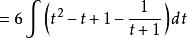有理代換

有理代換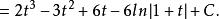

有理代換

有理代換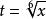

有理代換

有理代換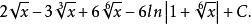

有理代換

有理代換

將代入，上式=