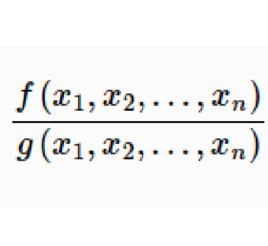定義
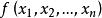 有理分式域
有理分式域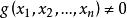 有理分式域
有理分式域有理分式域(field of rational fractions)是指包含多元多項式環的最小域。設與是數域P上的兩個n元多項式,
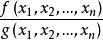 有理分式域
有理分式域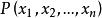 有理分式域
有理分式域稱為P上的 有理分式,亦稱 有理函式。與一元多項式的有理分式一樣,可以同樣地定義多元多項式的有理分式的加法與乘法,而且也滿足交換律、結合律與分配律.。數域P上任意兩個有理分式的和、差、積、商(除式不為零)仍為P上的有理分式。因此,P上的全體有理分式的集合構成一個域,稱為數域P上的 有理分式域,記為。
有理分式
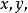 有理分式域
有理分式域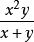 有理分式域
有理分式域有理分式(rational fraction)是兩多項式相除(作為除數的多項式次數不低於1)的一種表示式,含有除法且除式中含有變數字母的代數式稱為 有理分式,簡稱 分式。例如,對於變數字母代數式是有理分式,但
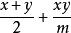 有理分式域
有理分式域是整式而不是有理分式,有理分式也可定義為一個多項式與一互素多項式的比
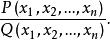 有理分式域
有理分式域在一個分式中被除式與除式分別稱為這個分式的分子與分母 。
有理分式的運算
和算術中的分數一樣,有理分式的運算分別定義如下 :
有理分式的加法
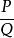 有理分式域
有理分式域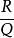 有理分式域
有理分式域兩個同分母有理分式和相加,只要把分子相加,分母不變:
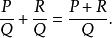 有理分式域
有理分式域對於異分母的有理分式相加,需要先進行通分,即把它們化成同分母的有理分式,然後再按同分母的有理分式的加法進行計算,運算的結果一般要化成既約分式:
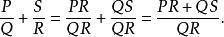 有理分式域
有理分式域和分數的加法一樣,有理分式的加法是滿足交換律和結合律的,即:
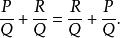 有理分式域
有理分式域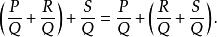 有理分式域
有理分式域有理分式的乘法
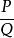 有理分式域
有理分式域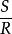 有理分式域
有理分式域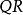 有理分式域
有理分式域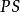 有理分式域
有理分式域兩個有理分式和相乘,把它們分母的積做積的分母,把它們分子的積做積的分子:
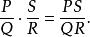 有理分式域
有理分式域當有理分式的分子和分母都是多項式時,先要各自進行因式分解然後再乘,並進行約分。或各自先進行約分,然後再乘。
在乘方運算中,先把有理分式的分子和分母各自因式分解,然後根據乘方法則展開,再求它們的積。
和分數的乘法一樣,有理分式的乘法是滿足交換律結合律以及乘法關於加法的分配律的。
有理分式的減法
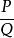 有理分式域
有理分式域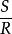 有理分式域
有理分式域對於任何有理分式來說,必定存在一個有理分式,滿足條件
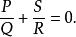 有理分式域
有理分式域兩個有理分式相減,如果是同分母,只要把分子相減,分母不變;如果是異分母,需要先進行通分,化成同分母的有理分式,然後再按同分母的有理分式相減計算。
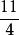 有理分式域
有理分式域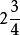 有理分式域
有理分式域在分數里可以把一個假分數化成帶分數。例如把化成。同樣,如果一個有理分式是假分式,也總可以把它化成帶分式,使所得的分式中分子的次數低於分母的次數,這樣,在運算過程中,較為簡便。
有理分式的除法
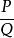 有理分式域
有理分式域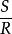 有理分式域
有理分式域有理分式的除法和有理分式的減法完全類似。有理分式中,P不是零多項式, 必定存在一個有理分式,滿足下列條件:
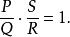 有理分式域
有理分式域有理分式的混合運算
有理分式的計算題里,如果有加、減、乘、除的混合運算,和在分數里做混合運算一樣,也是先乘除而後加減 。