名詞
現在被廣泛使用的數字修約規則主要有四捨五入規則和四捨六入五留雙規則。
註:經數值修約後的數值成為(原數值的)修約值。
內容
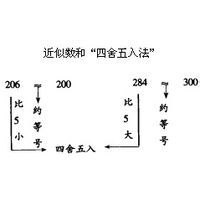
四捨五入
四捨五入是一種精確度的計數保留法,與其他方法本質相同。但特殊之處在於,採用四捨五入,能使被保留部分的與實際值差值不超過最後一位數量級的二分之一:假如0~9等機率出現的話,對大量的被保留數據,這種保留法的誤差總和是最小的。這大概也是我們使用這種方法為基本保留法的原因吧。
詳見詞條“四捨五入”。
四捨六入五單雙法
由於“四捨五入”造成“入得多,捨得少”的問題,給實際數據採集造成一定程度的不便。因此GB/T8170-2000的進舍規則規定為“四捨六入五單雙法”。
具體如下:
a)擬捨去的數字的最左邊一位數字小於5,則捨去,保留的數字不變;
例:將12.1498修約到個數位,得12;修約到一位小數,得12.1
b)擬捨去的數字的最左邊一位數字大於5,則進1,保留的數字最後一位加1;
例:將1268修約到“百”數位,得1300
c)擬捨去的數字的最左 邊一位數字是5,且其後面跟有非0數字時,則進1,保留的數字最後一位加1;
例:將10.5002修約到個數位,得11
d)擬捨去的數字的最右邊一位數字是5,且其後無數字或皆為0時,若保留數字的最後一位為奇數(1,3,5,7,9),則進1;保留數字的最後一位為偶數(0,2,4,6,8),則捨去。
例:將1.050修約到一位小數,得1.0;0.35修約到一位小數,得0.4
以上法則的口訣歸納為“四捨六入五考慮,五後非零則進一,五後皆零視奇偶,五前為偶應捨去,五前為奇應進一”