發展概況
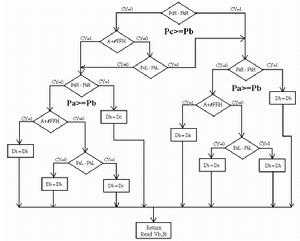二進制數常用的進制主要是十進制（因為我們有十個手指，所以十進制是比較合理的選擇，用手指可以表示十個數字，0的概念直到很久以後才出現，所以是1－10而不是0－9）。電子計算機出現以後，使用電子管來表示十種狀態過於複雜，所以所有的電子計算機中只有兩種基本的狀態，開和關。也就是說，電子管的兩種狀態決定了以電子管為基礎的電子計算機採用二進制來表示數字和數據。常用的進制還有8進制和16進制，在電腦科學中，經常會用到16進制，而十進制的使用非常少，這是因為16進制和二進制有天然的聯繫：4個二進制位可以表示從0到15的數字，這剛好是1個16進制位可以表示的數據，也就是說，將二進制轉換成16進制只要每4位進行轉換就可以了。
二進制的“00101000”直接可以轉換成16進制的“38”。一個字是電腦中的基本存儲單元，根據計算機字長的不同,字具有不同的位數，現代電腦的字長一般是32位的，也就是說，一個字的位數是32。位元組是8位的數據單元,一個位元組可以表示0－255的數據。對於32位字長的現代電腦，一個字等於4個位元組，對於早期的16位的電腦，一個字等於2個位元組。
特性
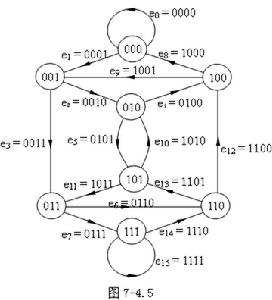二進制數2、如果一個二進制數的低端n位都是零，那么這個數可以被2n整除。
3、如果一個二進制數的第n位是一，而其他各位都是零，那么這個數等於2n。
4、如果一個二進制數的第零位到第n位（但不包含位n）都是一，而且其他各位都是零，那么這個數等於2n-1。
5、將一個二進制數的所有位左移移位的結果是將該數乘以二。
6、將一個無符號二進制數的所有位右移一位的結果等效於該數除以二（這對有符號數不適用）。餘數會被下捨入(rounddown)
7、將兩個n位的二進制數相成可能會需要2*n位來保存結果。
8、將兩個n位的二進制數相加或者相減絕不會需要多於n 1位來保存結果。
9、將一個二進制數的所有位取反（就是將所有的一改為零，所有的零改為一）等效於將該數取負（改變符號）再將結果減一。
10、將任意給定個數的位表示的最大無符號二進制數加一的結果永遠是零。
11、零遞減（減一）的結果永遠是某個給定個數的位表示的最大無符號二進制數。
12、n位可以表示2n個不同的組合。
13、數2年包含n位，所有位都是一。
運算
二進制數二進制數的四則運算
二進制數與十進制數一樣，同樣可以進行加、減、乘、除四則運算。其算法規則如下：
加運算：0 0=0，0 1=1，1 0=1，1 1=10，#逢2進1；
減運算：1-1=0，1-0=1，0-0=0，0-1=1，#向高位借1當2；
乘運算：0×0=0，0×1=0，1×0=0，1×1=1，#只有同時為“1”時結果才為“1”；
除運算：二進制數只有兩個數（0，1），因此它的商是1或0。
加法運算步驟如下：
（1）首先是最右數碼位相加。這裡加數和被加數的最後一位分別為“0”和“1”，根據加法原則可以知道，相加後為“1”。
（2）再進行倒數第二位相加。這裡加數和被加數的倒數第二位都為“1”，根據加法原則可以知道，相加後為“（10）2”，此時把後面的“0”留下，而把第一位的“1”向高一位進“1”。
（3）再進行倒數第三位相加。這裡加數和被加數的倒數第二位都為“0”，根據加法原則可以知道，本來結果應為“0”，但倒數第二位已向這位進“1”了，相當於要加“被加數”、“加數”和“進位”這三個數的這個數碼位，所以結果應為0 1=1。
（4）最後最高位相加。這裡加數和被加數的最高位都為“1”，根據加法原則可以知道，相加後為“（10）2”。一位只能有一個數字，所以需要再向前進“1”，本身位留下“0”，這樣該位相加後就得到“0”，而新的最高位為“1
二進制數（1）首先最後一位向倒數第二位借“1”，相當於得到了（10）2，也就是相當於十進制數中的2，用2減去1得1。
（2）再計算倒數第二位，因為該位同樣為“0”，不及減數“1”大，需要繼續向倒數第三位借“1”（同樣是借“1”當“2”），但因為它在上一步中已借給了最後一位“1”（此時是真實的“1”），則倒數第二位目前為1，與減數“1”相減後得到“0”。
（3）用同樣的方法倒數第三位要向它們的上一位借“1”（同樣是當“2”），但同樣已向它的下一位（倒數第二位）借給“1”（此時也是真實的“1”），所以最終得值也為“0”。
（4）被減數的倒數第四位儘管與前面的幾位一樣，也為“0”，但它所對應的減數倒數第四位卻為“0”，而不是前面幾位中對應的“1”，它向它的高位（倒數第五位）借“1”（相當於“2”）後，在借給了倒數第四位“1”（真實的“1”）後，仍有“1”余，1–0=1，所以該位結果為“1”。
（5）被減數的倒數第五位原來為“1”，但它借給了倒數第四位，所以最後為“0”，而此時減數的倒數第五位卻為“1”，這樣被減數需要繼續向它的高位（倒數第六位）借“1”（相當於“2”），2–1=1。
（6）被減數的最後一位本來為“1”，可是借給倒數第五位後就為“0”了，而減數沒有這個位，這樣結果也就是被減數的相應位值大小，此處為“0”。
在二進制數的加、減法運算中一定要聯繫上十進制數的加、減法運算方法，其實它們的道理是一樣的，也是一一對應的。在十進制數的加法中，進“1”仍就當“1”，在二進制數中也是進“1”當“1”。在十進制數減法中我們向高位借“1”當“10”，在二進制數中就是借“1”當“2”。而被借的數仍然只是減少了“1”，這與十進制數一樣。
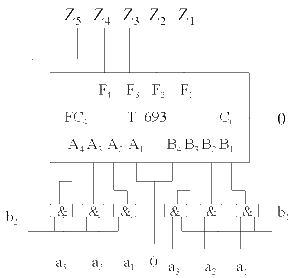二進制數乘法運算示例
把二進制數中的“0”和“1”全部當成是十進制數中的“0”和“1”即可。根據十進制數中的乘法運算知道，任何數與“0”相乘所得的積均為“0”，這一點同樣適用於二進制數的乘法運算。只有“1”與“1”相乘才等於“1”。乘法運算步驟：
（1）首先是乘數的最低位與被乘數的所有位相乘，因為乘數的最低位為“0”，根據以上原則可以得出，它與被乘數（1110）2的所有位相乘後的結果都為“0”。
（2）再是乘數的倒數第二位與被乘數的所有位相乘，因為乘數的這一位為“1”，根據以上原則可以得出，它與被乘數（1110）2的高三位相乘後的結果都為“1”，而於最低位相乘後的結果為“0”。
（3）再是乘數的倒數第三位與被乘數的所有位相乘，同樣因為乘數的這一位為“1”，處理方法與結果都與上一步的倒數第二位一樣，不再贅述。
（4）最後是乘數的最高位與被乘數的所有位相乘，因為乘數的這一位為“0”，所以與被乘數（1110）2的所有位相乘後的結果都為“0”。
（5）然後再按照前面介紹的二進制數加法原則對以上四步所得的結果按位相加（與十進制數的乘法運算方法一樣），結果得到（1110）2×（0110）2=（1010100）2。
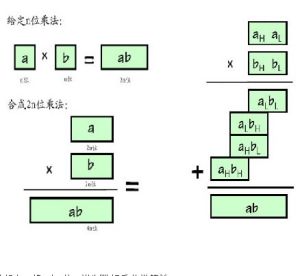二進制數（1）首先用“1”作為商試一下，相當於用“1”乘以除數“110”，然後把所得到的各位再與被除數的前4位“1001”相減。按照減法運算規則可以得到的餘數為“011”。
（2）因為“011”與除數“110”相比，不足以被除，所以需要向低取一位，最終得到“0111”，此時的數就比除數“110”大了，可以繼續除了。同樣用“1”作為商去除，相當於用“1”去乘除數“110”，然後把所得的積與被除數中當前四位“0111”相減。根據以上介紹的減法運算規則可以得到此步的餘數為“1”。
（3）因為“1”要遠比除數“110”小，被除數向前取一位後為“11”，仍不夠“110”除，所以此時需在商位置上用“0”作為商了。
（4）然後在被除數上繼續向前取一位，得到“110”。此時恰好與除數“110”完全一樣，結果當然是用“1”作為商，用它乘以除數“110”後再與被除數相減，得到的餘數正好為“0”。證明這兩個數能夠整除。
這樣一來，所得的商（1101）2就是兩者相除的結果。
轉換
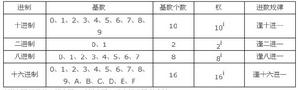各種數制表示的相互關係1．二進制與十進制間的相互轉換：
（1）二進制轉十進制
方法：“按權展開求和”
例：（1011.01）2
＝（1×23＋0×22＋1×21＋1×20＋0×2－1＋1×2－2）10
＝（8＋0＋2＋1＋0＋0.25）10
＝（11.25）10
規律：個位上的數字的次數是0，十位上的數字的次數是1，......，依獎遞增，而十分位的數字的次數是-1，百分位上數字的次數是-2，......，依次遞減。 注意：不是任何一個十進制小數都能轉換成有限位的二進制數。
（2）十進制轉二進制
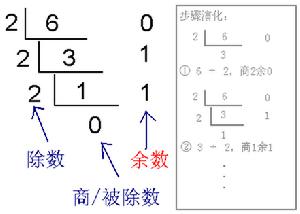
十進制整數轉二進制數：“除以2取余，逆序排列”（短除反取余法
例：（89）10＝（1011001）2
289
244……1
222……0
211……0
25……1
22……1
21……0
0……1
十進制小數轉二進制數：“乘以2取整，順序排列”（乘2取整法）
例：(0．625)10=(0．101)2
0．625
X2
1．251
X2
0．50
X2
1．01
二進制數二進制數轉換成八進制數：從小數點開始，整數部分向左、小數部分向右，每3位為一組用一位八進制數的數字表示，不足3位的要用“0”補足3位，就得到一個八進制數。
八進制數轉換成二進制數：把每一個八進制數轉換成3位的二進制數，就得到一個二進制數。
例：將八進制的37.416轉換成二進制數：
37．416
011111．100001110
即：（37.416）8＝（11111.10000111）2
例：將二進制的10110.0011轉換成八進制：
010110.001100
26.14
即：（10110.011）2＝（26.14）8
3．十六進制與二進制的轉換：
二進制數轉換成十六進制數：從小數點開始，整數部分向左、小數部分向右，每4位為一組用一位十六進制數的數字表示，不足4位的要用“0”補足4位，就得到一個十六進制數。
二進制數例：將十六進制數5DF.9轉換成二進制：
5DF．9
010111011111．1001
即：（5DF.9）16＝（10111011111.1001）2
例：將二進制數1100001.111轉換成十六進制：
01100001．1110
61．E
即：（1100001.111）2＝（61.E）16
4、整數的數制轉換
採用“基數除法”，具體步驟如下：
（1）將給定的十進制整數除以基數2，餘數便是等值的二進制的最低位。
（2）將上一步的商再除以基數2，餘數便是等值的二進制數的次低位。
（3）重複步驟2，直到最後所得的商等於0為止。各次除得的餘數，便是二進制各位的數，最後一次的餘數是最高
二進制
在日常生活中，我們常常使用各種編碼，如身份證號碼、電話號碼、郵政編碼等，這些編碼都是由十進制數組成的。
同理，在計算機中採用由若干位二進制數組成的編碼【簡稱二進制編碼】來表示字母、符號、漢字、顏色等非數值信息。
為了表示不同類型的信息，人們研究出了各種各樣的編碼方案。
ASCII碼（美國國家標準信息交換碼）
ASCII碼就是被普遍採用的一個英文字元信息編碼方案，它用8
位二進制數表示各種字母和符號，例如：
01000001表示A01000010表示B
8個二進制位稱為一個位元組（Byte，代號為B）。位元組是最基本的信息儲存單位，一個位元組可以儲存一個英文字母或符號編碼，兩個位元組可以儲存一個漢字編碼。
同二進制數一樣，二進制編碼也是計算機內部用來表示信息的一種手段，人們平時和計算機打交道時，根本不用理它。我們仍然用人們習慣的方式輸入或者輸出信息，期間的轉換則由計算機自動去完成。
計算機中一個存儲單位（即一個位元組）里存放的究竟是二進制數還是二進制編碼？是英文是漢字？事實上它們都由程式進行識別。例如，表示英文字元的8位二進制編碼的最高位是0，而表示漢字兩個8位二進制編碼的最高位是1，這一點就是程式區別存儲單位里存放的是英文還是漢字的一個依據。
漢字編碼
1980年中國為6763個常用漢字規定了編碼，稱為《信息交換用漢字編碼字元集·基本集》，簡稱GB2312-80，每個漢字占16位。在Windows95/98/2000/XP簡體中文版作業系統中，使用的是《漢字內碼擴展規範》，簡稱GBK，每個漢字占16位，它能表示20902個漢字。Linux簡體中文版作業系統中，使用的是UTF-8編碼，大多數漢字占24位，目前能表示7萬多個漢字。
實例對照
十進制數→二進制數
十進制
0
1
2
3
4
5
6
7
8
9
10
二進制
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
16→10000
46→101110
99→1100011
888→1101111000
7654→1110111100110
註：一般為了區別二進制數與十進制數，再二進制數後加上一個“B”，如145→10010001B
通常我們所說的數字，一般都是十進制，10分就1角，10角就1元……這些數字只是由十個數組成，那就是：0、1、2、3、4、5、6、7、8、9[我們一般稱之為基數(base)]
都是這些數，但它們處於不同位置所代表的重量就不一樣了喔，如111，都是1但就是不一樣，這就涉及到了位權的概念了，可用以下實例來說明。一個十進制數結4553.87可表示為：
在這個數中，有些相同的數字由於處在不同的位置，它們代表的數值的大小也不同，各位數字所代表的數值的大小是由位權來決定的。位權是一個乘方值，乘方的底數為進位計數制的基數（本例中為10），而指數由各位數字在數中的位置來決定。以上的十進制數中，從左至右各位數字的位權分別為：103、102、101、10o、、。一般而言，在進位制中，把一個數中各位數字為1時代表的數值大小稱為位權。如456它們的位權就是當各位為1時的數值大小，456中的4的位權就是10(2),5的位權就是10(1),6的位權就是10(0).
除了位權對於進制記數的另一個重要概念就是基數，基數很好理解，就是進位計數制中所使用的不同基本符號的個數稱為該計數制的基數，比如十進制就是1.2.3.4.5.6.7.8.9.0這十個數，相對而言二進制就兩個基數：0和1,八進制就是：0.1.2.3.4.5.6.7,十六進制就是：0.1.2.3.4.5.6.7.8.9.A.B.C.D.E.F
由上面兩個概念可以得出以下公式：[以下將詳細說名]
N進制的基數就能表示為：0、1、2、……、N-2、N-1
N進制的權一般可以表示：[X就是某數在它的數列中所處位置]
N進制展開成十進制公試：如
十進制：有10個基數：0、1、2、3、4、5、6、7、8、9，逢十進一
二進制：有2個基數：0、1，逢二進一
八進制：有8個基數：0、1、2、3、4、5、6、7，逢八進一
十六進制：有16個基數：0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F，逢十六進一
由於大家從小開始就學習十進制，生活中用途更是廣泛，一種單一的數字思維模式使我們很多人以為就只有這么一種進制數.在以下給大家說說計算機中用得最多的進制數，讓大家開闊思維，不要停留於一成不變的思維模式中。
計算機中用得最多也是CPU唯一能認出的數制，那就是二進制。計算機是處理信息的機器，信息處理的前提是信息的表示。計算機內信息的表示形式是二進制數字編碼。也就是說，各種類型的信息（數值、文字、聲音、圖像）必須轉換成數字量即二進制數字編碼的形式，才能在計算機中進行處理。那怕你移動一下滑鼠，按一下鍵盤，你的每一個動作最後到了CPU那也就只剩0和1了，有時覺得設計計算機的人也太厲害了，就兩個數字就能弄出這么完美的東西來，這就是智慧的結晶，其實說到底了CPU也就幾百條指令而已，在軟體和系統的層層迭加下讓我們根本就不了解計算機內部是什麼樣?其實沒什麼，就是0和1兩個狀態而已。
採用原因
容易表示
二進制數只有“0”和“1”兩個基本符號，易於用兩種對立的物理狀態表示。例如，可用"1"表示電燈開關的“閉合”狀態，用“0”表示“斷開”狀態；電晶體的導通表示“1”，截止表示“0”；電容器的充電和放電、電脈衝的有和無、脈衝極性的正與負、電位的高與低等一切有兩種對立穩定狀態的器件都可以表示二進制的“0”和“1”。而十進制數有10個基本符號（0、1、2、3、4、5、6、7、8、9），要用10種狀態才能表示，要用電子器件實現起來是很困難的。
運算簡單
二進制數的算術運算特別簡單，加法和乘法僅各有3條運算規則（0+0=0，0+1=1，1+1=10和0×0=0，0×1=0，1×1=1），運算時不易出錯。[其實計算機處理算術運算時都是加法和移位，並沒有乘除法，如11B左移一位就成了110B,11B是十進制的3，而110B是6，看看是不是等於乘二，左移乘，右移就除，哈哈，好玩吧]此外，二進制數的“1”和“0”正好可與邏輯值“真”和“假”相對應，這樣就為計算機進行邏輯運算提供了方便。算術運算和邏輯運算是計算機的基本運算，採用二進制可以簡單方便地進行這兩類運算。
