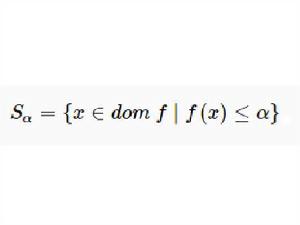基本概念
定義
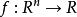 擬凸函式
擬凸函式函式 稱為擬凸函式(或者單峰函式),如果其定義域及所有下水平集
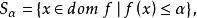 擬凸函式
擬凸函式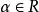 擬凸函式
擬凸函式 擬凸函式
擬凸函式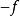 擬凸函式
擬凸函式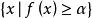 擬凸函式
擬凸函式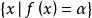 擬凸函式
擬凸函式,都是凸集。函式 是擬凹函式,如果 是擬凸函式,即每個上水平集 是凸集。若某函式既是擬凸函式又是擬凹函式,其為 擬線性函式。函式是擬線性函式,如果其定義域和所有的水平集 都是凸集。
 擬凸函式
擬凸函式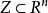 擬凸函式
擬凸函式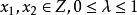 擬凸函式
擬凸函式定義1 設 定義域是凸集 ,若對於任意的 ,都有
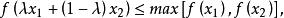 擬凸函式
擬凸函式 擬凸函式
擬凸函式則稱 在Z上是擬凸的。
 擬凸函式
擬凸函式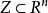 擬凸函式
擬凸函式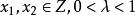 擬凸函式
擬凸函式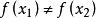 擬凸函式
擬凸函式定義2 設 其定義域 ,若對於任意 , 都有
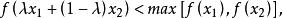 擬凸函式
擬凸函式 擬凸函式
擬凸函式則稱 在Z上是嚴格擬凸的。
 擬凸函式
擬凸函式 擬凸函式
擬凸函式若一 是擬凸(嚴格擬凸),則稱 是擬凹(嚴格擬凹)的。
 擬凸函式
擬凸函式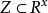 擬凸函式
擬凸函式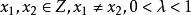 擬凸函式
擬凸函式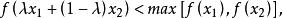 擬凸函式
擬凸函式 擬凸函式
擬凸函式定義3 設 其定義域 ,若對於任意的 ,都有 則稱 在Z上是強擬凸的。
 擬凸函式
擬凸函式 擬凸函式
擬凸函式若一 是強擬凸的,則稱 是強擬凹的。
對於定義在R上的函式,擬凸性要求每個下水平集是一個區間(有可能包括無限區間)。R上的一個擬凸函式如圖1所示。
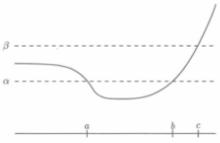 圖1
圖1 擬凸函式
擬凸函式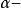 擬凸函式
擬凸函式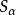 擬凸函式
擬凸函式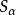 擬凸函式
擬凸函式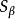 擬凸函式
擬凸函式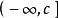 擬凸函式
擬凸函式圖1中R上的一個擬凸函式。對於任意 , 下水平集 是凸集,即某區間。下水平集 是區間[a,b]。下水平集 是區間 。
凸函式具有凸的下水平集,所以也是擬凸函式。但是擬凸函式不一定是凸函式。圖1所示的簡單例子即說明了這一點。
舉例說明
例1 R上的一些例子:
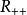 擬凸函式
擬凸函式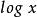 擬凸函式
擬凸函式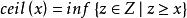 擬凸函式
擬凸函式對數函式:定義在 上的函式 是擬凸函式(也是擬凹函式,因此是擬線性函式)。上取整函式:函式 是擬凸函式(亦為擬凹函式)。
 擬凸函式
擬凸函式從上述例子可以看出,擬凸函式可能是凹函式,甚至有可能是不連續的。下面給出 上的一些例子。
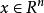 擬凸函式
擬凸函式例2向量的長度。定義 的長度為非零分量的下標的最大值,即
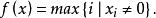 擬凸函式
擬凸函式(定義零向量的長度為零。)由於此函式的下水平集是子空間
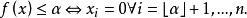 擬凸函式
擬凸函式 擬凸函式
擬凸函式所以它在 上是擬凸函式。
基本性質
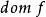 擬凸函式
擬凸函式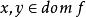 擬凸函式
擬凸函式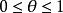 擬凸函式
擬凸函式在擬凸條件下,凸函式的很多性質仍然成立,或者可以找到類似性質。例如,存在一種變化的Jensen不等式來描述擬凸函式:函式f是擬凸函式的充要條件是, 是凸集,且對於任意 及 ,有
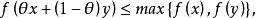 擬凸函式
擬凸函式即線段中任意一點的函式值不超過其端點函式值中最大的那個。上述不等式有時稱為擬凸函式的Jensen不等式,圖2所示即為一個擬凸函式的例子。
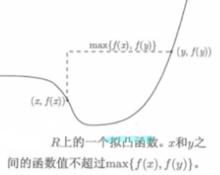 圖2
圖2 擬凸函式
擬凸函式 擬凸函式
擬凸函式和凸性類似,擬凸性可以由函式 在直線上的性質刻畫:函式 是擬凸的充要條件是它在和其定義域相交的任意直線上是擬凸函式。特別地,可以通過將一個函式限制在任意直線上,通過考察所得到的函式在R上的擬凸性來驗證原函式的擬凸性。
R上的擬凸函式
 擬凸函式
擬凸函式對R上的擬凸函式,我們給出一個簡單的刻畫。由於考慮一般的函式較為繁瑣,所以我們考慮連續函式。連續函式 是擬凸的,若且唯若下述條件至少有一個成立。
 擬凸函式
擬凸函式1.函式 是非減的;
 擬凸函式
擬凸函式2.函式 是非增的;
 擬凸函式
擬凸函式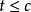 擬凸函式
擬凸函式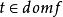 擬凸函式
擬凸函式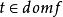 擬凸函式
擬凸函式 擬凸函式
擬凸函式3.存在一點 ,使得對於 (且 ),f非增,對於t≥c(且 ),f非減,點c可以在 的全局最小點中任選一個。圖3描述了這樣的情形。
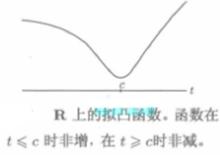 圖3
圖3相關定理
性質1
 擬凸函式
擬凸函式 擬凸函式
擬凸函式設 是強擬凸函式,則 是嚴格擬凸和擬凸函式。
但是嚴格擬凸函式不一定是擬凸函式,例如:
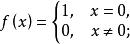 擬凸函式
擬凸函式它是嚴格擬凸,但它不是擬凸的。事實上,當函式是下半連續時,由嚴格擬凸性可推出擬凸性。
定理1
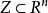 擬凸函式
擬凸函式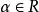 擬凸函式
擬凸函式設f是定義在凸集 上的實值函式,則對每個 ,f 的水平集都是凸集的充分必要條件是f是擬凸函式。
與凸函式相反,擬凸函式在它的定義域內部可以不連續,而且並非每個局部極小必是一個整體極小。
定理2
 擬凸函式
擬凸函式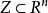 擬凸函式
擬凸函式 擬凸函式
擬凸函式 擬凸函式
擬凸函式設 在凸集 是擬凸函式,若 是f的一個嚴格局部極小值點,則 也是f在Z上的嚴格整體極小值。
定理3
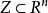 擬凸函式
擬凸函式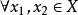 擬凸函式
擬凸函式設f 在開凸集 上是可微的,則f 是擬凸函式的充要條件是: ,若
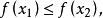 擬凸函式
擬凸函式必有
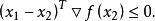 擬凸函式
擬凸函式定理4
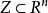 擬凸函式
擬凸函式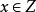 擬凸函式
擬凸函式設f在正則凸集 (有非空內部的凸集)上是擬凸的必要條件是:對每個 ,均有
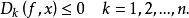 擬凸函式
擬凸函式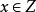 擬凸函式
擬凸函式類似的,擬凹的必要條件是:對每個 有
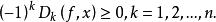 擬凸函式
擬凸函式定理5
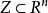 擬凸函式
擬凸函式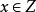 擬凸函式
擬凸函式設f在正則凸集 上,對每個 有
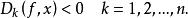 擬凸函式
擬凸函式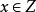 擬凸函式
擬凸函式則f 在Z上擬凸的,每個 有
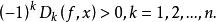 擬凸函式
擬凸函式則f在Z上是擬凹的。
定理6
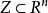 擬凸函式
擬凸函式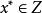 擬凸函式
擬凸函式 擬凸函式
擬凸函式設f在凸集 上的嚴格擬凸函式, 是f的一個局部極小值點,則 也是f在Z上的整體極小值點。