基本介紹
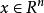 全局極小點
全局極小點定義1 若對於任意的,都有
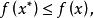 全局極小點
全局極小點 全局極小點
全局極小點 全局極小點
全局極小點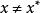 全局極小點
全局極小點 全局極小點
全局極小點 全局極小點
全局極小點則稱為的一個 全局極小點。若上述不等式嚴格成立且,則稱為的一個 嚴格全局極小點。
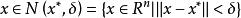 全局極小點
全局極小點定義2 若對於任意的,都有
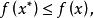 全局極小點
全局極小點 全局極小點
全局極小點 全局極小點
全局極小點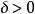 全局極小點
全局極小點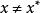 全局極小點
全局極小點 全局極小點
全局極小點 全局極小點
全局極小點則稱為的一個 局部極小點,其中為某個常數。若上述不等式嚴格成立且,則稱為的一個 嚴格局部極小點。
由上述定義可知,全局極小點一定是局部極小點,反之不然.一般來說,求全局極小點是相當困難的,因此,通常只求局部極小點(在實際套用中,有時求局部極小點已滿足了問題的要求) 。
全局極值
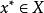 全局極小點
全局極小點 全局極小點
全局極小點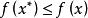 全局極小點
全局極小點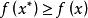 全局極小點
全局極小點 全局極小點
全局極小點 全局極小點
全局極小點 全局極小點
全局極小點 全局極小點
全局極小點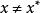 全局極小點
全局極小點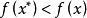 全局極小點
全局極小點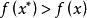 全局極小點
全局極小點 全局極小點
全局極小點 全局極小點
全局極小點 全局極小點
全局極小點全局極值(global extreme value)是實值函式在某區域取得極小或極大的值。設X為R中的集合,f為X上的實值函式,對於,如果對所有的均滿足(),則稱為在X上的 全局極小(大)點,為 全局極小(大)值。若對所有的,且,均有(),則稱為在X上的 嚴格全局極小(大)點,為 嚴格全局極小(大)值 。
凸函式的全局極小點
凸函式的極值(extreme value of convex function)是凸函式在某點鄰域(或某區域)內取得的極小值或極大值。凸函式的極值有以下性質:
 全局極小點
全局極小點1.若為定義在凸集S上的凸函式,則它的任一局部極小點就是它在S上的全局極小點,而且它的極小點形成一個凸集。
 全局極小點
全局極小點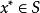 全局極小點
全局極小點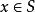 全局極小點
全局極小點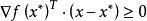 全局極小點
全局極小點 全局極小點
全局極小點 全局極小點
全局極小點2.設為定義在凸集S上的可微凸函式,若存在點,使得對於所有的,有,則是在S上的全局極小點。
3.定義在凸集上的凸函式的駐點(梯度為0的點),就是其全局極小點。全局極小點並不是惟一的,但若為嚴格凸函式,則其 全局極小點是惟一的 。