簡介
嚴格擬凸函式
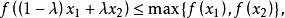嚴格擬凹函式設f是定義在實線性空間X的凸集K上的實值函式。如果對於任何x,x∈K和任何λ∈[0,1]，總有那么f就稱為K上的擬凸函式。
如果上述不等式是嚴格的，那么f就稱為K上的嚴格擬凸函式。
定義
如果-f是嚴格擬凸的，那么f就稱為嚴格擬凹函式。
凹函式
凹函式是數學模型中的一種，在數學當中，凹函式是凸函式的相反，是一個定義在某個向量空間的凸集C（區間）上的實值函式f。
設f為定義在區間I上的函式，若對I上的任意兩點X<X和任意的實數λ∈(0,1)，總有f(λx+(1-λ)x)≤λf(x)+(1-λ)f(x)，則f稱為I上的凹函式。
