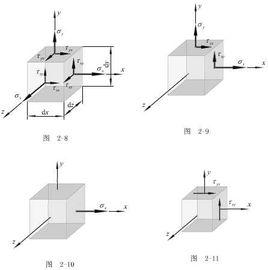
術語介紹
在變形體內原子 被迫偏離平衡位置,則該物體便出 現應力。所謂應力狀態就是物體內 的原子被迫偏離其平衡位置的狀 態。物體內各點產生屈服或斷裂都 和該點所受的應力狀態有關。為了 定性說明變形體內某點的應力狀 態,常採用主應力狀態圖示(簡稱應力圖示)。
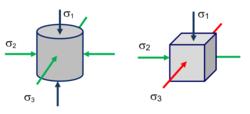 應力狀態
應力狀態應力狀態(stress state),物體受力作用時,其內部應力的大小和方向不僅隨截面的方位而變化,而且在同一截面上的各點處也不一定相同。通過物體內一點可以作出無數個不同取向的截面,其中一定可以選出三個互相垂直的截面,在它上面只有正應力作用,剪應力等於零,用這三個截面表達的某點上的應力,即稱為此點的應力狀態。
三個主應力不等且都不等於零的應力狀態稱為三軸(三維、空間)應力狀態;如有一個主應力等於零,則稱為雙軸(二維、平面)應力狀態;如有兩個主應力等於零則稱為單軸(或單向)應力狀態。
構件在受力時將同時產生應力與應變。構件內的應力不僅與點的位置有關,而且與截面的方位有關,應力狀態理論是研究指定點處的方位不同截面上的應力之間的關係。應變狀態理論則研究指定點處的不同方向的應變之間的關係。應力狀態理論是強度計算的基礎,而應變狀態理論是實驗分析的基礎。
如果已經確定了一點的三個相互垂直面上的應力,則該點處的應力狀態即完全確定。因此在表達一點處的應力狀態時,為方便起見,常將“點”視為邊長為無窮小的正六面體,即所謂單元體,並且認為其各面上的應力均勻分布,平行面上的應力相等。
分類表示
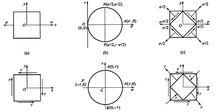 應力狀態
應力狀態可以證明,無論一點處的應力狀態如何複雜,最終都可用剪應力為零的三對相互垂直面上的正應力,即主應力表示。
三向應力狀態
當三個正應力均不為零時,稱該點處於三向應力狀態。若只有兩對面上的主應力不等於零,則稱為二向應力狀態或平面應力狀態。若只有一對面上的主應力不為零,則稱為單向應力狀態。
應力圓
應力圓是分析應力狀態的圖解法。
在已知一點處相互垂直的待定截面上應力的情況下,通過應力圓可求得該點處其他截面上的應力。應力圓也稱莫爾圓。
邊界條件
應力邊界條件
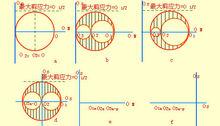 應力狀態
應力狀態應力邊界條件即彈性體在外力作用下處於平衡狀態的條件,是物體內部的各點的應力分量應滿足平衡方程式,物體邊界上各點也必須是平衡的。
由後者將導出應力邊界條件。換言之,所謂應力邊界條件就是在給定面力的邊界上應力分量與面力分量之間的關係。
混合邊界條件
混合邊界條件有兩種情況,一種情況是在物體的整個邊界s上,一部分為已知應力,即給定應力的邊界s ;另一種情況是在同一部分邊界上已知部分位移和部分應力,即給定位移與應力混合邊界條件。
應力偏量
在外力作用下,物體的變形通常可分為體積改變和形狀改變兩種成分,並且認為,體積的改變是由於各向相等的應力引起的。
實驗表明,同體材料在各向相等的應力作用下,一般都表現為彈性性質。因而可以認為材料的塑性變形主要是物體產生形狀變化時產生的。
所謂應力球張量 是一種平均的等向應力狀態(三向等拉或等壓),對各向同性材料,它引起微元體積膨脹或收縮。應力偏量表示實際應力狀態對其平均應力狀態的偏離,它引起微元形狀的改變。