莫爾圓

基本信息

• 中文名：莫爾圓
• 英文名：Mohr's Circle

• 別稱：莫爾應力圓
• 提出時間：1866年
• 提出者：K.庫爾曼
• 套用學科：數學、物理

概述

莫爾圓

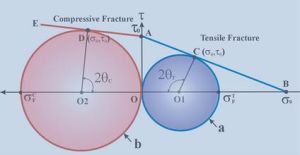在應力（或應變）坐標圖上表示受力（或變形）物體內一點中各截面上應力（或應變）分量之間關係的圓。表示應力的稱為應力莫爾圓；表示應變的稱為應變莫爾圓。

以平面應力為例說明二維應力莫爾圓的性質：受力物體內某一截面上的正應力σ 和剪應力τ 都是該截面法線與最大主應力σ1夾角θ的函式，可以分別用公式表示為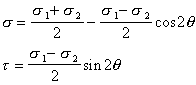

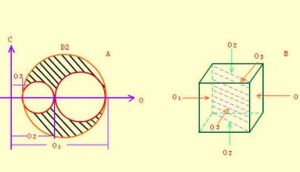式中σ1 和 σ2為兩個主應力。這兩個關係式也可以用莫爾圓上N點的坐標值（見圖）來表示，N點與σ1 夾圓心角為2θ。 當(σ1和σ2為已知時, 用公式法或莫爾圓法都可獲得通過該點的任一截面上的正應力和剪應力值。莫爾圓法的操作是：取σ 為橫坐

莫爾圓

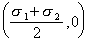標，τ為縱坐標，在橫坐標上分別取量值為σ1 和σ2 的兩點,取兩點間的中點為圓心作圓，則此圓的圓心坐標為 ，圓半徑值為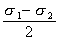。如果欲知道法線與σ1 夾角為θ的截面上的正應力和剪應力，可從 σ1 開始，量得圓心角為2θ而獲得N點,則N點的橫坐標恰好為該截面上的正應力值，N點的縱坐標恰好為該截面的剪應力值。N點的橫坐標值等於圓心的橫坐標值加上半徑值與cos2θ之積，即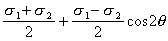，與公式的結果一樣；N點的縱坐標值等於半徑值與sin2θ之積，即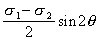，與公式的結果也一樣。改變θ角就可以獲得任意截面上的正應力與剪應力值。當 2θ=90°或270°時，其最大的縱坐標值即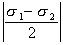，它表示法線與最大主應力分別夾45°和135°的截面上剪應力最大,但兩者有相反的符號。當2θ=0或者180°，恰好是σ1 和σ2 兩點,這兩點的縱坐標值為零, 表示主應力作用面上沒有剪應力，而且σ1與σ2之間夾角θ=90°，即彼此永遠垂直。

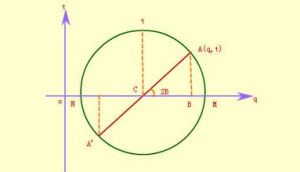莫爾圓

莫爾圓法方便而且直觀,是變形分析的良好工具,從而在地質研究中得到廣泛的套用。與此同時應變莫爾圓也為應變分析提供了方便。三維莫爾圓可以分析物體內三維空間任意截面上的應力或者應變關係。應變莫爾圓以及三維應力（或應變）莫爾圓都是以二維應力莫爾圓為基礎建立的，它們與二維應力莫爾圓的分析方法類似。
參考書目
W.D.米恩斯著，丁中一等譯：《應力和應變》，科學出版社，北京，1982。(W.D.Means,Stress and Strain,Springer-Verlag,New York,1976.)

性質

莫爾圓

二向應力下的性質 二向應力狀態的莫爾圓有如下性質：①莫爾圓上每一點的坐標都對應於單元體上某一截面上的正應力和剪應力；②若莫爾圓上的兩個點組成的圓心角為2α),則單元體上相應的兩個截面的外法向的夾角為α,且角度的轉向相同。根據上述性質，以單元體上某個面為基面，以莫爾圓上與該面對應的點為基點，就能求出單元體中各截面上的應力,或找出最大剪應力面和主平面(即剪應力為零的平面)的方向。
三向應力下的性質三向應力狀態的莫爾圓是在已知物體上一點的三個主應力σ1、σ2、σ3的前提下得到的。即莫爾圓給出了一點的應力範圍。若已知截面的法向與三個主應力方向的夾角或方向餘弦，也可通過幾何方法確定出該截面上正應力和剪應力的值。但在一般工程套用中，知道應力範圍就足夠了。對於應變，也有相同形式的莫爾圓。