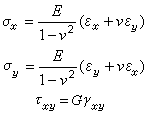應力狀態和應變狀態
正文
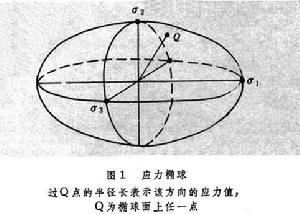
構件在受力時將同時產生應力與應變。構件內的應力不僅與點的位置有關,而且與截面的方位有關,應力狀態理論是研究指定點處的方位不同截面上的應力之間的關係。應變狀態理論則研究指定點處的不同方向的應變之間的關係。應力狀態理論是強度計算的基礎,而應變狀態理論是實驗分析的基礎。應力狀態 如果已經確定了一點的三個相互垂直面上的應力,則該點處的應力狀態即完全確定。因此在表達一點處的應力狀態時,為方便起見,常將“點”視為邊長為無窮小的正六面體,即所謂單元體,並且認為其各面上的應力均勻分布,平行面上的應力相等。單元體在最複雜的應力狀態下的一般表達式如圖1,諸面上共有9個應力分量。可以證明,無論一點處的應力狀態如何複雜,最終都可用剪應力為零的三對相互垂直面上的正應力,即主應力表示。當三個正應力均不為零時,稱該點處於三向應力狀態。若只有兩對面上的主應力不等於零,則稱為二向應力狀態或平面應力狀態。若只有一對面上的主應力不為零,則稱為單向應力狀態。
 應力狀態和應變狀態
應力狀態和應變狀態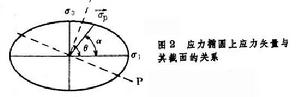 應力狀態和應變狀態
應力狀態和應變狀態廣義胡克定律 當按材料線上彈性範圍內工作時,一點處的應力狀態與應變狀態之間的關係由廣義胡克定律表達。對於各向同性材料,彈性模量E、剪下彈性模量G、泊松比v均與方向無關,且線應變只與正應力σ有關,剪應變只與剪應力τ有關。三向應力狀態下,各向同性材料的廣義胡克定律為
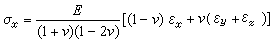
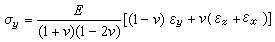
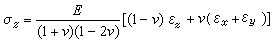
τxy=Gγxy
τyz=Gγyz
τzx=Gγzx
平面應力狀態(σz=0, τyz=0, γzx=0)下的廣義胡克定律套用最為普遍