概念
基本公式
自重應力是指由岩石自重引起的應力。
 自重應力
自重應力 自重應力
自重應力公式: = · z
 自重應力
自重應力:土的天然重度,kN/m;
z:土的深度,m;
基本算法
1)Haim法則(靜水壓力理論)
 自重應力
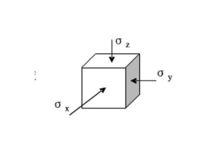
自重應力瑞士地質學家Haim在觀察了大型越嶺隧道圍岩工作狀態之後,認為原岩體鉛垂應力為上覆岩體自重。在漫長的地質年代中,由於岩體不能承受較大的差值應力和與時間有關的變形的影響,使得水平應力與鉛垂應力趨於均衡的靜水壓力狀態。
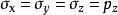 自重應力
自重應力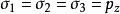 自重應力
自重應力由於靜水壓力下無剪應力,所以任意方向都是主應力方向。
2)金尼克解(彈性側壓理論)
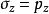 自重應力
自重應力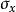 自重應力
自重應力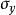 自重應力
自重應力金尼克認為地下岩體為線彈性體,其鉛垂應力等於上覆岩體自重: 在水平方向,岩層內的側向應力 與 相等,且水平方向的應變為零:
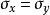 自重應力
自重應力 自重應力
自重應力由廣義虎克定律:
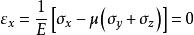 自重應力
自重應力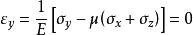 自重應力
自重應力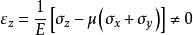 自重應力
自重應力則可解出:
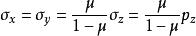 自重應力
自重應力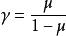 自重應力
自重應力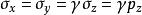 自重應力
自重應力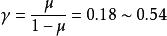 自重應力
自重應力令 ,側向壓力係數則有: 。一般岩石的泊松比μ=35.0~15.0,因此 。當μ=5.0時,γ=1,則金尼克公式與Haim法則一致。
平行層狀岩體的自重應力場
岩體中原始地應力的確定是採礦、水利等地下工程中非常重要而又複雜的課題。岩石應力的測試手段和分析方法還遠遠不能滿足工程需要,主要是由於岩石材料極端複雜的性質限制了測試與分析理論的發展。地殼表層的岩石多數為沉積岩,層理、層面、節理等地質構造,使岩體呈現明顯的各向異性。在地應力研究中,考慮這種各向異性的工作曾有人做過,進展十分緩慢,主要的困難有兩點:即建立合適的各向異性力學解答,以及岩體參數的確定。值得關心的問題是:如果岩體的各向異性對地應力分布規律和測試有根本性的影響,那么,就需要考慮岩體的各向異性。Amadei等的研究適合分析正交各向異性參數對水平或鉛垂層狀岩體自重應力場的影響。研究將平行層狀岩體視為等效的橫觀各向同性體,研究了岩層傾斜時傾角和彈性參數分別對自重應力場的影響。結果表明,水平應力受岩層傾角的影響很明顯,且隨著傾角的變化,水平應力受岩體參數的影響規律也不同。
平行層狀岩體自重應力場
為便於層狀岩體中區域應力場的研究,假定所研究的岩體層面是相互平行的,各個岩層的厚度與區域尺寸相比很小,因此,可將岩體視為等效的均勻、橫觀各向同性線彈性材料,而各向同性平面就與各岩層層面平行。這種等效材料的 5個獨立彈性常數依賴於各個岩層的彈性參數和厚度,詳細討論可見文獻。
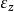 自重應力
自重應力文獻針對水平或鉛垂層狀岩體在自重荷載作用的條件下作了如下假定:岩體內部各點沿水平方向位移為零,沿鉛垂方向(z向)位移僅是坐標z的函式。從而得到岩體內部各點的應變狀態為 不等於0其餘5個應變分量都為零。當岩層傾斜時,上述假定就過於嚴格。
研究結論
在自重荷載作用下,各向同性岩體內的最大主應力總是鉛垂的,並且兩個水平主應力相等。對於橫觀各向同性岩體,分析結果表明:
(1)鉛垂應力雖然亦是主應力,但不一定是最大主應力;
(2)由大量計算結果總結出側壓係數的範圍一般是0<k<1.5,0<k<1.5;
(3)隨著岩層傾角的變化,兩個水平主應力可能會從相等到相差幾倍。
地應力研究工作不僅包括現場實測以及對測試資料的分析,從理論上對較大範圍的地應力狀況進行分析也十分必要,因為地下坑道的開挖尺度遠大於測試鑽孔的尺度,由於岩體不均勻性的客觀存在,必然導致地應力狀況的尺度效應。因此,在對層狀岩體的等效各向異性參數研究的基礎上,利用本文的理論解,可以對岩體基本呈平行層狀分布時的區域應力場進行分析。當岩體內有複雜的地質構造時,本文解答不適用,但本文的結論指出了在分析重力應力場時各向異性參數及岩層傾角的重要影響,對具體的複雜問題可藉助數值計算來完成進一步的分析工作。
土的自重應力和有效自重應力
20世紀 80 年代,在某刊進行過土的自重應力和有效自重應力的討論:一位同行發表一篇短文認為自重應力計算時水下部分自重應按飽和重度計算,該文的觀點遭到很多人的反對,這些人認為土的自重應力應是有效應力。該刊從反對這種觀點的文章中選擇了一篇予以發表並加了編者按。又有一些學者在《岩土工程界 》進行了這樣的討論,不過仍然沒有達成一致,甚至產生了一些新問題。看來,關於土的自重應力和有效自重應力的討論離迷的破解還有相當長的距離。
關於土的自重應力的定義
陳津民先生對土的自重應力的定義是: “土被看成普通的線彈性體且無主動面力時土自重這個體力的彈性應力解。”但自重應力與是否把土看成普通的線彈性體無關(非線性的彈性體、非彈性體也有應力),也不能理解為某種條件下的應力解。自重應力計算方法才與對土的材料性質假定有關。在定義中,自重應力應歸結於應力(或單位面積截面上的內力)而不是應力解。土的自重應力就是土體中由土的自重引起的應力或者說就是土體中由土的自重引起的單位面積截面上的內力。這就是土的自重應力的定義。
關於土的自重應力的計算
土的自重應力計算方法與對土的材料性質的假定、對土層結構的假定、對土體表面形態的假定有關,具體計算公式還與截面方向有關。在地基計算中,通常是在土為線彈性材料、土體為表面水平的半無限空間、土層沿水平方向無限展布的假定下計算土的自重應力的,並主要計算土的豎向自重正應力。在這些假定下,土的豎向自重剪應力恆為0而無需計算,故土的豎向自重正應力可簡稱為土的豎向自重應力;在不計算土的側向自重應力的場合還可以進一步簡稱為土的自重應力。
根據上述土的自重應力的定義和計算假定,土的豎向自重應力就是土體中單位面積底面的土柱重量引起的壓力。它是土的重度與土柱高度(即計算點從地面起算的深度)之積或各層土的重度與相應層土柱高度乘積之和。重度因含水量的增高而增大。如果把水下的土視為飽和,那么水下土的重度就增大到最大值—飽和重度。按照上述土的自重應力定義和計算假定,土的自重應力有以下有別於附加應力的特點: 1)豎向自重應力和側向自重應力均是主應力;2)自重應力不小於0(但這不表示其改變數不小於0) 。3)自重應力隨土的重度與土柱高度的增大而增大;4)自重應力來源單一(即來自土的自重)。因此,土的豎向自重應力計算與附加應力計算不同,是簡單的加法計算,不存在求矢量和及代數和的問題。
關於土的有效自重應力的定義
土的有效自重應力是一種有效應力,在一般情況下不能簡稱為土的自重應力,在不可能引起混淆的場合(如不涉及地下水和地表水的場合)才可簡稱為土的自重應力。其概念來源於有效應力原理。不僅其計算必須遵循有效應
力原理,其定義也必須遵循有效應力原理。因此,土的有效自重應力的定義應該是土的自重應力中能引起土體變形的那部分應力或者說是土的自重應力中的有效部分。
當計算由土的自重引起的土體變形時,必須計算土的有效自重應力。但不計算土的自重應力,就無從計算土的有效自重應力;沒有土的自重應力,就沒有土的有效自重應力。因此,土的自重應力和有效自重應力這兩個概念都是需要的,只提土的自重應力而不提(或否定)土的有效自重應力或者只提土的有效自重應力而不提(或否定)土的自重應力都是片面的。
關於土的有效自重應力的計算
按照有效應力原理,對飽和土,總應力等於有效應力與孔隙水應力之和,也就是說,總應力分為有效應力與孔隙水應力(它是總應力中的無效部分即中性部分)兩部分,或者說,有效應力與孔隙水應力是總應力的兩個組成部分。總體中的部分不可能超過總體,如:土分為粗粒土和細粒土,一個場地粗粒土的數量和細粒土的數量不可能超過土的數量。因此,有效應力與孔隙水應力都不可能超過總應力。
在土的有效自重應力計算中,總應力是自重應力,對飽和土,自重應力等於有效自重應力與孔隙水應力(它是自重應力中的無效部分即中性部分,故準確地說應稱為初始孔隙水應力)之和。因此,有效自重應力計算有以下原則:1)計算中涉及的總應力與孔隙水應力均應屬於自重應力;2)孔隙水應力應是無效應力即中性應力;3)有效自重應力不應超過自重應力。有了這些原則就可以對有效自重應力計算是否應考慮滲流、毛細水應力、結合水應力、下方承壓水水應力的影響用出判斷。

