描述
在數學中，微分運算元是定義為微分運算之函式的運算元。首先在記號上，將微分考慮為一個抽象運算是有幫助的，它接受一個函式得到另一個函式（以計算機科學中高階函式的方式）。
當然也有理由不單限制於線性運算元；例如施瓦茨導數是一個熟知的非線性運算元。不過這裡只考慮線性情形。
記號
最常用的微分運算元是取導數自身。這個運算元的常用記號包括：d/dx,D，這裡關於哪個變數微分是清楚的，以及D，這裡指明了變數。一階導數如上所示，但當取更高階 n-次導數時，下列替代性記號是有用的：d /dx ,D ,D 。
記號 D的發明與使用歸於奧利弗·亥維賽，他在研究微分方程中考慮了如下形式的微分運算元
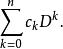微分運算元另一個最常見的微分運算元是拉普拉斯運算元，定義為
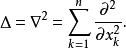微分運算元另一個微分運算元是Θ運算元，定義為
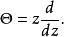微分運算元有時候這也稱為齊次運算元，因為它的本徵函式是關於 z的單項式：
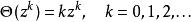微分運算元在 n個變數中齊次運算元由
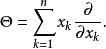微分運算元給出。與單變數一樣，Θ的本徵空間是齊次多項式空間。
性質
（1）微分是線性的，即
D(f+g)=(Df)+(Dg)
D(af)=a(Df)
這裡 f和 g是函式，而 a是一個常數。
（2）任何以函式為係數之 D的多項式也是一個微分運算元。我們也可以通過法則
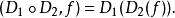微分運算元（3）複合微分運算元。需要一些注意：首先運算元 D中的任何函式係數必須具有 D所要求的可微次數。為了得到這樣運算的一個環，我們必須假設所用的係數的所有階導數。第二，這個環不是交換的：一個運算元 gD一般與 Dg不同。事實上我們有例，如在量子力學中的基本關係：
Dx-xD=1
但這些運算元的子環： D的常係數多項式是交換的。它可以另一種方式刻畫：它由平移不變運算元組成。
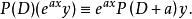微分運算元（4）微分運算元也服從移位定理（shift theorem），即
運算元的伴隨
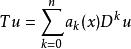微分運算元
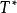微分運算元給定一個線性微分運算元 T，，這個運算元的伴隨定義為運算元使得
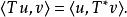微分運算元
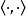微分運算元這裡記號表示數量積或點積。從而此定義取決於數乘的定義。
單變數
在平方可積函式空間中，數量積定義為
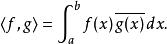微分運算元
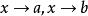微分運算元如果另外增添要求 f或 g當等於零，我們也可定義 T的伴隨為
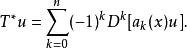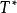微分運算元 微分運算元此公式不明顯地取決於數量積的定義，故有時作為伴隨運算元的一個定義。當用這個公式定義時，它稱為 T的 形式伴隨。
一個（形式） 自伴運算元是與它的（形式）伴隨相等的運算元。
多變數
如果Ω是 R中一個區域，而 P是Ω上一個微分運算元，則 P在 L(Ω)中的伴隨由對偶性以類似的方式定義：
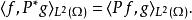微分運算元對所有光滑 L函式 f與 g。因為光滑函式在 L中是稠密的，這在 L的一個稠密子集上定義了伴隨：: P是一個稠定運算元。
例子
施圖姆-劉維爾運算元是形式自伴運算元一個熟知的例子。這個二階微分運算元 L可以寫成如下形式
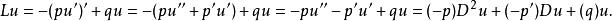微分運算元這個性質可用上面的形式自伴的定義來證明。
套用
•在物理科學的套用中，像拉普拉斯運算元在建立與求解偏微分方程中起著主要的作用。
•在微分拓撲中，外導數與李導數運算元有內蘊意義。
•在抽象代數中，導子的概念是微分運算元不要求分析的一個推廣。通常這樣的推廣用於代數幾何與交換代數。
相關條目
•差分運算元
•Delta operator
•橢圓型運算元
•分數微積分
•不變微分運算元
