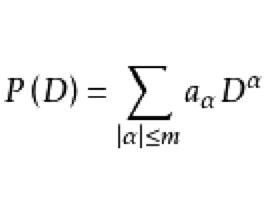基本介紹
常係數微分運算元是係數為常數的線性偏微分運算元,其一般形式為:
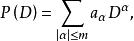 常係數微分運算元
常係數微分運算元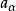 常係數微分運算元
常係數微分運算元其中 為常數(實數或複數)。例如,拉普拉斯運算元
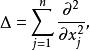 常係數微分運算元
常係數微分運算元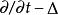 常係數微分運算元
常係數微分運算元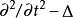 常係數微分運算元
常係數微分運算元熱運算元 ,波運算元 等都是常係數微分運算元。線性偏微分運算元理論中的若干重要問題,如基本解的存在性、局部可解性、亞橢圓性的判定等對於常係數情形均已完全解決 。
基本解的存在性定理
 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元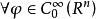 常係數微分運算元
常係數微分運算元基本解的存在性定理(theorem for existence offundamental solution)是關於基本解存在性的一個定理。該定理斷言:每個非零的常係數微分運算元 都有基本解, 的基本解E作為廣義函式可如下構造: ,
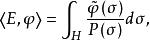 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元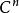 常係數微分運算元
常係數微分運算元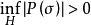 常係數微分運算元
常係數微分運算元其中 表示 的逆傅立葉變換。H為 中某個適當的區域,滿足 ,由基本解的存在可知常係數微分運算元是局部可解運算元。
亞橢圓常係數微分運算元
 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元亞橢圓常係數微分運算元(hypoelliptic differential operator with constant coefficients)是最基本的亞橢圓運算元,設 是常係數微分運算元,則下述條件中的每一個都是 為亞橢圓運算元的充分必要條件:
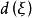 常係數微分運算元
常係數微分運算元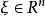 常係數微分運算元
常係數微分運算元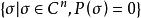 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元1.以 記 集合 的距離,則當 時, 。
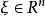 常係數微分運算元
常係數微分運算元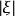 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元2.存在正的常數c及C,當 且 充分大時,不等式 成立。
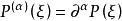 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元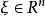 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元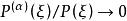 常係數微分運算元
常係數微分運算元3.記 ,對於每個非零多重指標 ,當 且 時,有 。
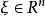 常係數微分運算元
常係數微分運算元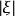 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元4.存在正的常數c及C,當 且 充分大時,不等式 成立 。
施瓦茲定理
 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元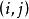 常係數微分運算元
常係數微分運算元施瓦茲定理[Schwarz(th.de)]設 為 的開集 上的連續可微的數值函式,且在 的點 處兩次可微,則對 的任一相異元素偶 ,必有
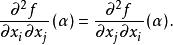 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元這個定理表明,在 上無限可微的全體函式之向量空間 的全體自同態之代數中,所有自同態
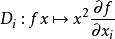 常係數微分運算元
常係數微分運算元兩兩可交換。因此,由這些自同態生成的酉子代數是交換的;它的元素是常係數微分運算元 。
定強微分運算元
 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元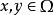 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元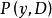 常係數微分運算元
常係數微分運算元對 定義的微分運算元稱為在中 具定強,若對任意固定的,常係數微分運算元及是等強的,即
 常係數微分運算元
常係數微分運算元下面的引理把這個條件改成通常更方便的形式。
 常係數微分運算元
常係數微分運算元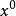 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元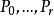 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元引理1 設具定強,對固定的令並設是弱於的常係數運算元的有限維向量空間的基底,則有
 常係數微分運算元
常係數微分運算元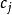 常係數微分運算元
常係數微分運算元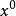 常係數微分運算元
常係數微分運算元 常係數微分運算元
常係數微分運算元這裡係數唯一確定,在為0且有與的係數相同的可微性及連續性質 。