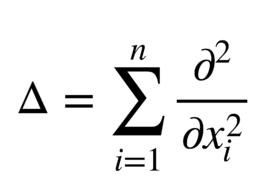定義
拉普拉斯運算元是 n維歐幾里德空間中的一個二階微分運算元，定義為梯度（▽f）的散度（▽·f）。因此如果 f是二階可微的實函式，則 f的拉普拉斯運算元定義為：
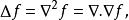拉普拉斯運算元
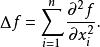拉普拉斯運算元f的拉普拉斯運算元也是笛卡爾坐標系 x i中的所有 非混合二階偏導數：
作為一個二階微分運算元，拉普拉斯運算元把 C函式映射到 C函式，對於 k≥2時成立。運算元Δ : C( R) → C( R)，或更一般地，定義了一個運算元Δ : C(Ω) → C(Ω)，對於任何開集Ω時成立。
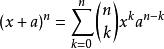拉普拉斯運算元函式的拉普拉斯運算元也是該函式的黑塞矩陣的跡 ：
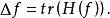拉普拉斯運算元另外，滿足▽·▽f=0 的函式f, 稱為調和函式。
表示式
二維空間
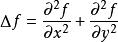拉普拉斯運算元其中 x與 y代表 x-y 平面上的笛卡爾坐標：
另外極坐標的表示法為：
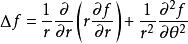拉普拉斯運算元
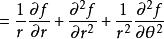拉普拉斯運算元三維空間
笛卡爾坐標系下的表示法
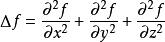拉普拉斯運算元圓柱坐標系下的表示法
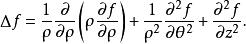拉普拉斯運算元球坐標系下的表示法
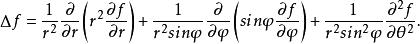拉普拉斯運算元N 維空間
在參數方程為（其中以及）的 N維球坐標系中，拉普拉斯運算元為：
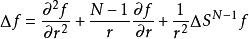拉普拉斯運算元其中是 N− 1維球面上的拉普拉斯-貝爾特拉米運算元。
橢圓型偏微分方程
[elliptic partial differential equation]
橢圓型偏微分方程是偏微分方程的一個類型，簡稱橢圓型方程。這類方程主要用來描述物理中的平衡穩定狀態，如定常狀態的電磁場、引力場和反應擴散現象等。
橢圓型方程是由方程中主部的係數來界定的。對兩個自變數的二階線性或半線性方程
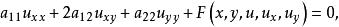拉普拉斯運算元
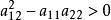拉普拉斯運算元在不等式 成立的區域內，就稱方程是橢圓型的。此時，可以通過自變數的非奇異變換將方程化為標準型
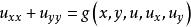拉普拉斯運算元。
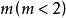拉普拉斯運算元對於高階線性方程，設 階線性偏微分運算元為
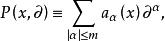拉普拉斯運算元
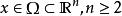拉普拉斯運算元
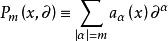拉普拉斯運算元
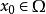拉普拉斯運算元
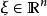拉普拉斯運算元
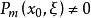拉普拉斯運算元
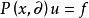拉普拉斯運算元
拉普拉斯運算元
拉普拉斯運算元 拉普拉斯運算元其中， 。該偏微分運算元的主部是 若對 及任意非零向量 都有 ，則稱方程 在點 是橢圓型的。如果在 中每一點都是橢圓型的，就稱該方程在 中是線性橢圓型方程。
線型橢圓型方程的典型代表是拉普拉斯方程（也叫調和方程）
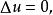拉普拉斯運算元
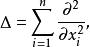拉普拉斯運算元其中， 這個運算元叫拉普拉斯運算元（Laplace operator），也叫調和運算元。可以說，調和方程是最基本，同時也是最重要的線性橢圓型方程。
對於非線性方程，也可以定義橢圓型方程。例如，考慮二階實係數擬線性方程
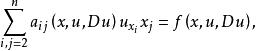拉普拉斯運算元
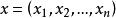拉普拉斯運算元
拉普拉斯運算元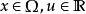
拉普拉斯運算元
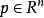拉普拉斯運算元其中， 。如果對任意非零向量 ， 及 ，有
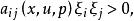拉普拉斯運算元 拉普拉斯運算元就稱方程是 中的擬線性橢圓型方程。類似地，可以定義高階擬線性橢圓型方程。
推廣
拉普拉斯運算元可以用一定的方法推廣到非歐幾里德空間，這時它就有可能是橢圓型運算元，雙曲型運算元，或超雙曲型運算元。
在閔可夫斯基空間中，拉普拉斯運算元變為達朗貝爾運算元。
達朗貝爾運算元通常用來表達克萊因-高登方程以及四維波動方程。
