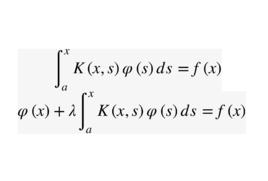沃爾泰拉積分方程

沃爾泰拉積分方程與弗雷德霍姆積分方程的不同之處，許多數學物理問題需通過積分方程或微分方程求解，積分方程是近代數學的一個重要分支。

定義

形如

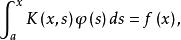沃爾泰拉積分方程

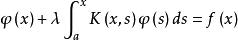沃爾泰拉積分方程

沃爾泰拉積分方程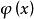

沃爾泰拉積分方程

的積分方程分別稱為第一類和第二類沃爾泰拉積分方程，其中， 是參數， 是未知函式。這是沃爾泰拉（V.Volterra）在研究某個生態平衡問題時提出並討論的積分方程。

弗雷德霍姆積分方程

形如

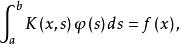沃爾泰拉積分方程

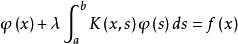沃爾泰拉積分方程

的積分方程分別稱為第一類和第二類弗雷德霍姆積分方程。

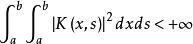沃爾泰拉積分方程

其中，λ是參數，φ(x)是未知函式，。

辨析

沃爾泰拉積分方程

第二類沃爾泰拉積分方程沒有特徵值，是區別於弗雷德霍姆積分方程的重要特點。對於任意的右端，方程都有唯一解，並且解可以表示為

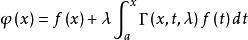沃爾泰拉積分方程

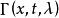沃爾泰拉積分方程

其中， 為方程的解核。

沃爾泰拉積分方程與弗雷德霍姆積分方程的不同之處，僅在於它的積分上限是變數x，且α≤y≤x≤b，此處α、b是常量。沃爾泰拉積分方程可視為弗雷德霍姆積分方程的核K(x,y)當y>x時為零的情形。