廣義單側導數

廣義單側導數是單側導數的推廣。廣義單側導數又分為廣義左導數和廣義右導數。 若f在a處連續，則廣義單側導數即為單側導數。

簡介

廣義單側導數是單側導數的推廣。

若f在a處連續，則廣義單側導數即為單側導數。  

廣義左（右）導數

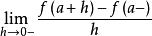廣義單側導數

設實函式f在a∈R的某個左領域內有定義且左極限f(a-)存在，若極限存在，則此極限稱為f在a處的廣義左導數，記為f'_(a-)或f'_(a-0)。

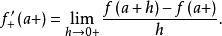廣義單側導數

類似的，定義廣義右導數

單側導數

函式的導數實際上是一種特殊形式的函式極限。函式有左、右極限的概念，因此也可以定義函式在一點的左、右導數。對於分段函式，如何判斷它在分段點處的可導性，就要用到在分段點處的左、右導數。

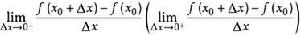廣義單側導數

設函式y=f(x)在x點及其一個左（右）領域(x-δ,x)（(x,x+δ)）有定義。如果極限存在，則稱此極限為函式f(x)在點x的左（右）導數，左右導數統稱為單側導數。