定義
 迪尼導數
迪尼導數 迪尼導數
迪尼導數 迪尼導數
迪尼導數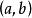 迪尼導數
迪尼導數設 是 上的實值函式, 是 內的一點,令
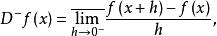 迪尼導數
迪尼導數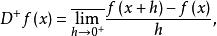 迪尼導數
迪尼導數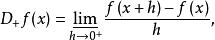 迪尼導數
迪尼導數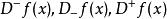 迪尼導數
迪尼導數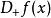 迪尼導數
迪尼導數 迪尼導數
迪尼導數 迪尼導數
迪尼導數 迪尼導數
迪尼導數 迪尼導數
迪尼導數(1) 我們將 和 這四個廣義實數依次稱為 是在 的 左上導數、左下導數、右 上導數和 右下導數;統稱為 在 的 迪尼導數。
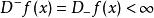 迪尼導數
迪尼導數 迪尼導數
迪尼導數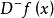 迪尼導數
迪尼導數 迪尼導數
迪尼導數 迪尼導數
迪尼導數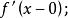 迪尼導數
迪尼導數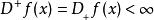 迪尼導數
迪尼導數 迪尼導數
迪尼導數 迪尼導數
迪尼導數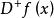 迪尼導數
迪尼導數 迪尼導數
迪尼導數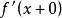 迪尼導數
迪尼導數(2) 若 ,則稱 在 左可微,並稱 為 在點 的 左導數,記 若 ,則稱 在 右可微,並稱 為 在 的 右導數,記作 。
 迪尼導數
迪尼導數 迪尼導數
迪尼導數顯然可導四個迪尼導數存在且相等。
相關結論
由迪尼導數的定義可知:
 迪尼導數
迪尼導數 迪尼導數
迪尼導數 迪尼導數
迪尼導數 迪尼導數
迪尼導數 迪尼導數
迪尼導數1. 在點 可微若且唯若 在 的四個迪尼導數相等且是實數;若且唯若 在點x既左可微又右可微且 。
 迪尼導數
迪尼導數2. 當 為單調遞增函式時,f是在x的四個迪尼導數都是非負的廣義實數;當f為單調遞減函式時,f是在x的四個迪尼導數都是非正的廣義實數 。
迪尼導數的提出
1914-1916年間, 格蕾絲·西斯霍姆·楊在各類國際期刊上發表了一系列獨立署名的關於微分學基礎的論文。1914年,她的《關於導數和微分係數的註解》(A Note on DerivativesandDifferentialCofficients)發表在瑞典刊物《數學活動》(Acta Mathematica) 上,闡述了一些關於導數特殊性質的初步結果。
 迪尼導數
迪尼導數 迪尼導數
迪尼導數1915年她的論文《關於無窮導數》贏得了哥頓學院的“博彩獎”。這篇較長的專題論文1916 年發表在《純粹與套用數學季刊》(QuarterlyJournal of Pure and Applied Mathematics) 上,討論了連續但不可導的函式。在繼續她的研究主題後,另一篇較短的論文《關於一個方程的導出數》(On the numbersderived from a function)發表在同一年的《科學院每周會議記錄譯本》上。1916 年,《倫敦數學會公報》發表了她的題為《關於一個函式的導數》(On theDerivatives of a Function)的論文,她在其中討論了一個函式的4 種經典導數變分(variation),即左上、左下、右上、右下迪尼導數(Dini derivation)。她對連續函式和可測(measurable)函式的4 個迪尼導數行為作出分類。她闡明,除去一些點,4 個迪尼函式只能具有3種行為:全等;兩個正無窮,兩個負無窮;或一個正無窮,一個負無窮,另兩個為某個相同有限值。她所證明的結果與法國數學家阿諾德當儒瓦(Arnaud Denjoy)和波蘭數學家史丹尼勞薩克斯(Stanislaw Saks)的相似結果一起並稱為當儒瓦-薩克斯-楊定理。這個定理使研究者可以利用排除法,即通過證明第二三種情形不會發生來判定一個特定的函式是可導的。
1915年,楊夫婦從日內瓦搬到了瑞士的另一個城市洛桑,但這並沒有妨礙學術多產的楊。在20世紀20 年代,她繼續發表著變分方面的論文。在1919年發表在《數學科學簡報》(Bllein of the mathematical scence)的“在不使用康托數下對勒貝格引理的證明”( Demonstration of Lebesgue's lemma without the use of theCantor numbers)中,她寫到了勒貝格積分。她1922年的“關於黎曼定理的註解”(A Note on a Theorem of Riemann's) 發表在《數學簡訊》(Messenger ofMathematics) 上。1922年她還在《倫敦數學會公報》上發表了《關於多變數函式的偏導數》(On the Partial Derivatives of a Function of Many Variables)討論多變數變分。《數學基礎》(Fundamenta Mathematicae) 於1929年刊發了她的《關於可微函式》(On Functions Possessing Differentials)。
楊在20世紀20年代的文章不只是變分,其中有兩篇是有感於古希臘哲學家柏拉圖(Plato)的數學思想。1924 年在《倫敦數學會公報》上發表《一對聯立丟番圖方程組的解法與柏拉圖聯姻數》(On the Solution of a Pairof SimultaneousDiophantine Equations Connected with the Nuptial Number in Plato)。5 年之後,她又與丈夫合寫了《摘自柏拉圖家美諾篇的經世之謎》(A Time-HonouredMystery from the Meno of Plato),發表在《歐傳統》(O tradition)。1926年她為一本教育期刊寫了一篇說明性的文章,介紹希臘數學家畢達哥拉斯(Pythagoras)和他那著名的關於直角三角形三邊長關係的定理。這篇文章題為(畢達哥拉斯,他怎樣證明他的定理?》(How did he prove his theorem),發表在《數學教育》(Mathematics education)上 。