廣義柯西公式

簡介

廣義柯西公式亦稱廣義柯西型積分，是解析函式柯西公式的推廣。

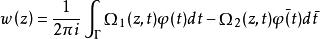廣義柯西公式

設φ(z)是Γ上的連續函式，則稱為廣義柯西型積分。

推導

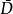廣義柯西公式

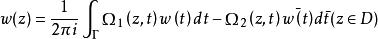廣義柯西公式

以 D 表示複平面的有界多連通區域，其邊界Γ是有限條逐段光滑的簡單閉曲線，設w(z)是在上連續的廣義解析函式，則有廣義柯西公式其中，Ω(z,t)，Ω(z,t)稱為廣義解析函式的基本核。

基本核條件

基本核條件滿足條件：

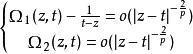廣義柯西公式

這裡p(>2)是正常數。

解析函式

解析函式是區域上處處可微分的複函數。17世紀，L.歐拉和J.leR.達朗貝爾在研究水力學時已發現平面不可壓縮流體的無旋場的勢函式Φ(x,y)與流函式Ψ(x,y)有連續的偏導數，且滿足微分方程組，並指出f(z)=Φ(x,y)+iΨ(x,y)是可微函式，這一命題的逆命題也成立。

柯西把區域上處處可微的複函數稱為單演函式，後人又把它們稱為全純函式、解析函式。B.黎曼從這一定義出發對複函數的微分作了深入的研究，後來，就把上述的偏微分方程組稱為柯西-黎曼方程，或柯西-黎曼條件。