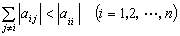對角優勢矩陣

一個矩陣，如果其每一行的非對角元的模之和都小於這一行的對角元的模，即稱該矩陣是嚴格對角優勢或強對角優勢（ strictly diagonally dominant ）的。

對角優勢矩陣

正文

一個n×n階矩陣A＝(αij)，如果其每一行的非對角元的模之和都小於這一行的對角元的模，即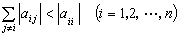

，

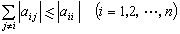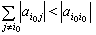
就稱A是嚴格對角優勢或強對角優勢的；若A僅滿足

，

但至少有一個下標i =i0使

成立,就稱A是弱對角優勢的。這類矩陣有著廣泛的實際背景，如很多微分方程邊值問題的離散化方程的係數矩陣往往具有上面的性質，因此對這類矩陣的研究是十分重要的。這類矩陣還有一些重要性質,例如，若矩陣A是嚴格對角優勢或不可約弱對角優勢的，則 A是非奇異的；若A還是埃爾米特矩陣，且對角元皆為正數，則A是正定的。又如用直接法或疊代法解係數矩陣為對角優勢矩陣的線性代數方程組時，可以保證算法的穩定性或收斂性。
參考書目
　R.S.瓦格著，蔣爾雄等譯：《矩陣疊代分析》,上海科學技術出版社,上海，1966。(R.S.Varga,Matrix Iterative Analysis,Prentice-Hall, Englewood Cliffs, New Jersey, 1962.)
　D.M.Young,Iterative Solution of large Linear Systems, Academic Press, New York, 1971.

配圖

相關連線