定義
矩陣中非零元素的個數遠遠小於矩陣元素的總數，並且非零元素的分布沒有規律，通常認為矩陣中非零元素的總數比上矩陣所有元素總數的值小於等於0.05時，則稱該矩陣為稀疏矩陣(sparse matrix)，該比值稱為這個矩陣的稠密度；與之相區別的是，如果非零元素的分布存在規律（如上三角矩陣、下三角矩陣、對角矩陣），則稱該矩陣為特殊矩陣。
比較基本的定義是矩陣中的大多數元素為零，並且可以利用零元素節約大量存儲、運算和程式運行時間。
簡介
稀疏矩陣幾乎產生於所有的大型科學工程計算領域，包括計算流體力學、統計物理、電路模擬、圖像處理、納米材料計算等。
存儲格式
最常用的稀疏矩陣存儲格式為列壓縮存儲(compressedcolumn storage,CCS) 或行壓縮存儲( ompressedrow storage,CRS)。
稀疏矩陣以CCS 格式為例，一個 階包含 nnz 個非零元的稀疏矩陣需要用列指針、行指標和非零值三個一維數組表示，其中 nnz 維非零值數組按列記錄所有非零元素，同樣維數的行指標記錄每列非零元所在的行，n+1 維的列打針向量記錄每一列(包括 n+1 列) 的開始位置。還有三元組表和連結存儲等其他格式等。
一個對稱或埃爾米特稀疏矩陣可以節約將近一半的存儲量。
符號稀疏矩陣(symbolic sparse matrix) 只需列指針和行指標兩個數組。此外，稀疏向量是稀疏矩陣的特例，只需用指標和非零值兩個數組表示，最近在電路、電子結構等領域得到越來越多的重視。
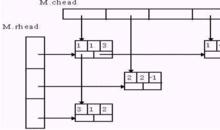圖1.稀疏矩陣的壓縮存儲優點
稀疏矩陣的計算速度更快，因為 MATLAB 只對非零元素進行操作，這是稀疏矩陣的一個突出的優點。
假設矩陣 A,B 中的矩陣一樣，計算 2*A 需要一百萬次的浮點運算，而計算 2*B 只需要 2000 次浮點運算。
因為 MATLAB 不能自動創建稀疏矩陣，所以要用特殊的命令來得到稀疏矩陣。算術和邏輯運算都適用於稀疏矩陣。
對於一個用二維數組存儲的稀疏矩陣 Amn ，如果假設存儲每個數組元素需要 L 個位元組，那么存儲整個矩陣需要 m*n*L 個位元組。但是，這些存儲空間的大部分存放的是 0 元素，從而造成大量的空間浪費。為了節省存儲空間，可以只存儲其中的非 0 元素。
圖2.對於矩陣 A 的每個元素 a ，知道其行號 i 和列號 j 就可以確定其位置。因此對於稀疏矩陣可以用一個結點來存儲一個非 0 元素。該結點可以定義：[i,j,a]。該結點由3個域組成，i：行號，j：列號，a元素值。
這樣的結點被稱為三元組結點。矩陣的每一個元素 Q，由一個三元組結點 (i,j,a) 唯一確定。
運算
稀疏矩陣和稠密向量的乘積運算等相對容易實現。稀疏矩陣和稠密向量的高性能運算類似，它可以通過對行列的適當排序實現，其中塊操作起著至關重要的作用。
對稀疏矩陣結構的操作則比較複雜，和排序、消去數等圖論技巧關係密切，比如稀疏矩陣的求和與三角分解會產生填充（fill-in），兩個稀疏矩陣的乘積的高效實現至今仍是一個具有挑戰性的問題。另一方面，稀疏矩陣運算，比如三角分解，還要考慮數值穩定性問題，稀疏性和數值穩定性往往是一對矛盾。
有些套用問題，尤其是有限元離散化得到的稀疏矩陣，往往具有非常特殊的結構，在區域和格線均勻等條件下可以實現快速算法。
