基本概念
命題
命題的定義:一般的,在數學中把用語言、符號或式子表達的,可以判斷真假的陳述句叫做命題。其中判斷為真的語句叫做真命題,判斷為假的語句叫做假命題。
每一個命題都有逆命題,只要將原命題的題設改成結論,並將結論改成題設,便可得到原命題的逆命題。但是原命題正確,它的逆命題未必正確。例如真命題“對頂角相等”的逆命題為“相等的角是對頂角”,此命題就是假命題。
互逆命題
互逆命題的定義:如果一個命題的條件與結論分別是另一個命題的結論與條件,那么這兩個命題稱為互逆命題。如把其中一個稱為原命題,那么另一個稱為它的逆命題。其中一個命題稱為另一個命題的逆命題。把一個命題的條件和結論互換就得到它的逆命題,所以每個命題都有逆命題。
逆否命題
逆否命題的定義:一個命題的條件和結論分別是另一個命題的條件的否定和結論的否定,把這樣的兩個命題叫做互否命題。如果把其中一個稱為原命題,那么另一個就叫做它的否命題。
等價命題的引入
原命題、逆命題、否命題和逆否命題四種命題有如下關係,如圖1其所示:
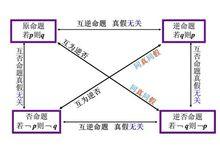 圖1
圖1(1)原命題與逆命題互逆;
(2)否命題與原命題互否;
(3)原命題與逆否命題相互逆否;
(4)逆命題與否命題相互逆否;
(5)逆命題與逆否命題互否;
(6)逆否命題與否命題互逆 。
這四種命題的真假關係如下表所示:
| 原命題 | 逆命題 | 否命題 | 逆否命題 |
| 真 | 真 | 真 | 真 |
| 真 | 假 | 假 | 真 |
| 假 | 真 | 真 | 假 |
| 假 | 假 | 假 | 假 |
兩個命題為互逆命題或互否命題,它們的真假性沒有關係;兩個命題互為逆否命題,它們有相同的真假性(原命題與逆否命題同真同假,逆命題與否命題同真同假)。由此,可以引出等價命題的概念,從而有:互為逆否的兩個命題是等價命題。
等價命題的簡介
等價命題,即同一意思不同說法,就是兩個命題的條件本質上是相同的,結論在本質上也是相同的,等價的命題只有形式上的不同。 等價命題就是說兩個命題可以相互證明。 即如果 A,B 兩個命題等價,那么, 把 A 命題作為條件,可以證明 B命題;同時,把 B 命題作為條件,也可以證得 A 命題。
注意等價命題並不對要比較的兩個命題的真偽性做討論, 只是對兩個命題的相互關係做討論,即兩個假命題也可以相互等價。例如:命題 A:3>5,命題 B:2<0 ,那么這兩個命題就是等價的, 運用簡單的不等式知識, 這兩個命題可以互推。等價性的本質是在一定的範圍內討論兩個命題的相同性,即他們是相同或是不同的(等價或不等價的)。
一般,原命題與其逆否命題互為等價命題 。
利用等價命題解題
由命題 A(或問題 A)可推出命題 B(或問題 B),反之,命題 B(或問題 B)亦可推出命題 A(或問題 A).即 A與 B 互為充要條件時,稱為 A 與 B 等價.利用這種等價性將原命題(或原問題)轉化成易於處理的新命題(或新問題)的方法稱為等價法。
產生等價命題 (或問題) 經常通過以下幾種途徑: 更換等價的條件 (或已知) 和結論(或所求);通過適當的代換;利用原命題與逆否命題的等價關係。
(1)利用等價命題判斷充要性:對於以否定形式給出的數學命題,若直接判定語句之間的充要關係難度較大,可根據原命題與其逆否命題等價,判斷其逆否命題,則問題可迎刃而解。
(2)利用命題的等價關係進行同解變形:在數學中, 存在許許多多具有等價性的問題, “同解變形” 是解題的最基本的方法, 如解方程和不等式的過程本身就是一個同解轉化的過程。
(3)利用命題的等價關係實現“正難則反”:如果一個命題從正面解決不好入手或比較麻煩,可以從命題的反面入手來解決,即所謂的反證法.反證法正是基於原命題與其逆否命題等價的思想。如:證明命題的唯一性、無理性,或所給的命題以否定形式出現 (如: 不存在、 不相交等),並伴有 “至少”“不都”“都不”“沒有”等指示性詞語時,均可考慮用反證法的思想來實現轉化。
(4)利用命題的等價關係實現數形轉換:數形結合的思想就是把問題的數量關係和幾何圖形結合起來加以考察的思想,其實質就是把抽象的數量關係和直觀的圖形結合起來,從而降低原命題的難度,使問題容易得到解決。
等價轉化是一種重要的數學思想,數學問題的求解過程事實上是一個不斷轉化的過 程,這種過程體現了“把未知解法的問題化歸到在已有知識範圍內可解”的求解策略。化歸轉化分等價轉化與非等價轉化兩種情況。當轉化過程中的前因後果是既充分又必要時,則稱這種轉化為等價轉化。
