簡介
在代數學中， 胡爾維茲定理（又名“1,2,4,8定理”）是以在1898年證明它的阿道夫·胡爾維茲命名。該定理表明：任何帶有單位元的賦范可除代數同構於以下四個代數之一：R,C,H和O，分別代表實數、複數、四元數和八元數。對實賦范可除代數的分類始於弗洛比紐斯，發揚於胡爾維茲，由佐恩整理為一般形式。一個簡短的歷史摘要可見Badger。
完整的證明能在凱特和索洛多斯尼科夫或者夏皮羅處找到。一個基本的想法是，如果一個代數 A是成正比於1的，那么它同構於實數。否則，我們使用凱萊-迪克森結構擴展子代數以同構於1，並引入一個向量正交於1。此子代數是同構於複數的。如果它不是 A的全體，那么我們再次使用凱萊-迪克森結構和另一個與複數正交的向量，得到一個與四元數同構的子代數。如果這還不是不是 A的全體，我們重複以上行為一次，並得到同構於凱萊數（或八元數）的子代數。我們現在有一個定理，說的是每一個包含1而又不是 A自身的子代數是結合的。凱萊數不是結合的，因此必須為 A。
胡爾維茲定理也可以用於證明n個平方和與n個平方和的積仍可以寫成n個平方和僅當n為1,2,4或者8時。
凱萊-迪克森結構
在數系理論中， 凱萊-迪克森構造以定義在實數集的代數結構為基礎構造出新的代數系統序列。序列中每一個代數系統的維度都是其前一個的2倍。所有通過該過程產生的代數系統，即所謂的凱萊-迪克森代數系。它擴展了複數的概念，屬於超複數的範疇。
凱萊-迪克森構造的代數系統中，都有範數和共軛的概念。從廣義的概念上講，集合中的一個元素和它的共軛的乘積等於它的範數的平方。
一個有趣的現象是，在凱萊-迪克森構造的代數系統序列中的每一個代數系統比起其前一個系統，除了有一個更高的維度數之外，都將失去前一個系統所擁有的一個特定性質。
賦范可除代數
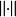胡爾維茲定理在數學中，一個 賦范可除代數A是一個在實數域或複數域上的可除代數，它同時還是一個賦范線性空間，這裡範數滿足下面的性質：
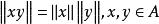胡爾維茲定理儘管定義允許賦范可除代數是無限維的，但事實上並沒有。僅有的實數域上的賦范可除代數（在同構意義下）有
•實數，記號為R
•複數，記號為C
•四元數，記號為H
•八元數，記號為O
這一結論被稱為胡爾維茲定理。在所有以上情形中，範數由絕對值給出。注意，前三種是結合代數，而八元數是交錯代數（結合性的一種弱形式）。唯一的複數域上的賦范可除結合代數是複數域自身。賦范可除代數是合成代數的一種特殊情況。合成代數是具有可乘的二次型的麼代數。通常的合成代數不必是可除的，相反，它可能含有零因子。實數域上的合成代數提供了三種額外的代數：分裂複數、分裂四元數和分裂八元數。
