定義
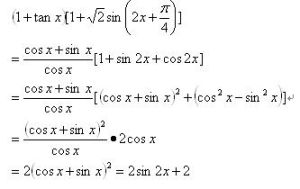 域
域第二種定義,設 ;是環,如果 ;和 ;都是交換群,則稱 ;是域。比如:有限整數環 ;必是域。
典型域
有理數域(Q,+,*), 實數域(R,+,*),複數域(C,+,*),連續函式域(R^R,+,·)etc但整數集Z不是域,因為1/x不是整數。(整數集Z是一個環,更準確的說是整環)
![域[數學辭彙] 域[數學辭彙]](/img/f/533/nBnauM3XxEjMxkTM1UDOwATN2QTM1UTM4UjNyQTNwAzMwIzL1gzLygzLt92YucmbvRWdo5Cd0FmLxE2LvoDc0RHa.jpg)
域,代數學中的基本概念。在環的概念基礎上,如果集合還具有除法及相應的運算性質,就稱為域。域之原義指範圍,是語境可以隨著認知不斷擴展的詞。後逐漸演變為數學、生物、科技等學科的某類單位的分類詞語。
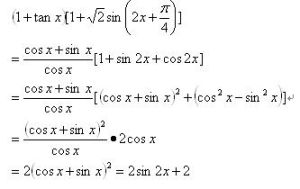 域
域域,代數學中的基本概念。在環的概念基礎上,如果集合還具有除法及相應的運算性質,就稱為域。域之原義指範圍,是語境可以隨著認知不斷擴展的詞。後逐漸演變為數學...
字形字義 數學辭彙(Field) 生物學辭彙(Domain) 計算機辭彙中域教育集團是一家集醫師資格考試、考研高端、公務員考試為一體的教學研究的專業化、規模化的考前輔導機構。自成立以來,業務領域擴展了二十省,培訓學員15萬名...
簡介 培訓理念 獲得榮譽 師資團隊美國高考SAT在改革之後,數學部分的考題範圍與難易程度有所提高。以前的SAT數學考試程度僅相當於國內初三的數學水平,主要考學生的四則運算、因數、分數、百...
SAT數學考試內容 SAT數學考察學生的何種能力? 分數算法: SAT數學邏輯推理解題法fraction fraction rea
圖書信息 內容簡介 作者簡介 目錄 序言《數學物理方程與特殊函式》是一本於1999年7月1日高等教育出版社出版的圖書。
圖書信息 目錄《三等分角與數域擴充》是2004年湖南教育出版社出版的圖書,作者是李尚志。
內容提要 編輯推薦 目錄若干重大問題研究》《中學生材料作文》《高考改革新視點叢書》(語文、數學...
選擇題及寫作,主要測驗考生的閱讀、數學及寫作能力 滿分 2400分 SAT2...。 SAT2是單科考試,有數學、物理、化學、生物、外語(包括漢語、日語、德語...。 3.SAT考試加試題說明 加試部分是不固定的,分析性閱讀,數學,語法...
SAT簡介 SAT1與SAT2的區別 SAT閱讀考試技巧 SAT數學 SAT語法備考重點