切線簡介
幾何上,切線指的是一條剛好觸碰到曲線上某一點的直線。更準確的說,當切線經過曲線上的某點(即切點)時,切線的方向與曲線上該點的方向是相同的,此時,“切線在切點附近的部分”最接近“曲線在切點附近的部分”(無限逼近思想)。tangent在拉丁語中就是to touch的意思。類似的概念也可以推廣到平面相切等概念中。
曲線切線和法線的定義
P和Q是曲線C上鄰近的兩點,P是定點,當Q點沿著曲線C無限地接近P點時,割線PQ的極限位置PT叫做曲線C在點P的切線,P點叫做切點;經過切點P並且垂直於切線PT的直線PN叫做曲線C在點P的法線(無限逼近的思想)
說明:平面幾何中,將和圓只有一個公共交點的直線叫做圓的切線.這種定義不適用於一般的曲線;PT是曲線C在點P的切線,但它和曲線C還有另外一個交點;相反,直線l儘管和曲線C只有一個交點,但它卻不是曲線C的切線.
切線性質
切線的性質定理
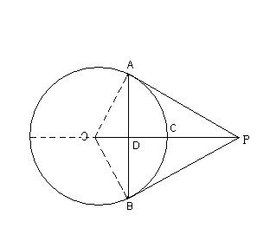
推論1:經過圓心且垂直於切線的直線必經過切點.
推論2:經過切點且垂直於切線的直線必經過圓心.
切線的主要性質
(1)切線和圓只有一個公共點;
(2)切線和圓心的距離等於圓的半徑;
(3)切線垂直於經過切點的半徑;
(4)經過圓心垂直於切線的直線必過切點;
(5)經過切點垂直於切線的直線必過圓心;
(6)從圓外一點引圓的切線和割線,切線長是這點到割線與圓交點的兩條線段長的比例中項
其中(1)是由切線的定義得到的,(2)是由直線和圓的位置關係定理得到的,(6)是由相似三角形推得的,也就是切割線定理。
切線的判定和性質
切線的判定定理 經過半徑的外端並且垂直於這條半徑的直線是圓的切線 。圓的切線垂直於這條圓的半徑。
幾何語言:∵l ⊥OA,點A在⊙O上
∴直線l是⊙O的切線(切線判定定理)
切線的性質定理 圓的切線垂直於經過切點半徑
幾何語言:∵OA是⊙O的半徑,直線l切⊙O於點A
∴l ⊥OA(切線性質定理)
推論1 經過圓心且垂直於切線的直徑必經過切點
推論2 經過切點且垂直於切線的直線必經過圓心
切線長定理
定理 從圓外一點引圓的兩條切線,它們的切線長相等,圓心和這一點的連線平分兩條切線的夾角
幾何語言:∵弦PB、PD切⊙O於A、C兩點
∴PA=PC,∠APO=∠CPO(切線長定理)
弦切角
弦切角定理 弦切角等於它所夾的弧對的圓周角
幾何語言:∵∠BCN所夾的是 ,∠A所對的是
∴∠BCN=∠A
推論 如果兩個弦切角所夾的弧相等,那么這兩個弦切角也相等
幾何語言:∵∠BCN所夾的是 ,∠ACM所對的是 , =
∴∠BCN=∠ACM
弦切角概念:頂點在圓上,一邊和圓相交、另一邊和圓相切的角叫做弦切角.它是繼圓心角、圓周角之後第三種與圓有關的角.這種角必須滿足三個條件:
(1)頂點在圓上,即角的頂點是圓的一條切線的切點;
(2)角的一邊和圓相交,即角的一邊是過切點的一條弦所在的射線;
(3)角的另一邊和圓相切,即角的另一邊是切線上以切點為端點的一條射線.
它們是判斷一個角是否為弦切角的標準,三者缺一不可,比如下圖中 均不是弦切角.
(4)弦切角可以認為是圓周角的一個特例,即圓周角的一邊繞頂點鏇轉到與圓相切時所成的角.正因為如此,弦切角具有與圓周角類似的性質.
弦切角定理:弦切角等於它所夾的孤對的圓周角.它是圓中證明角相等的重要定理之一.
切割線定理:從圓外一點引圓的切線和割線,切線長是這點到割線與圓交點的兩條線段長的比例中項。
推論:從圓外一點引圓的兩條割線,這一點到每條割線與圓的交點的兩條線段長的積相等。