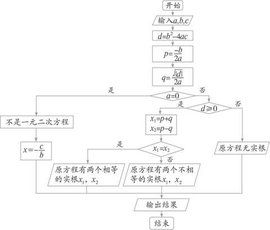
步驟
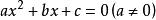公式法1.化方程為一般式：
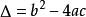公式法2.確定判別式，計算Δ（希臘字母，音譯為戴爾塔）。；
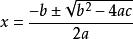公式法3.若Δ>0，該方程在實數域內有兩個不相等的實數根：；
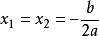公式法若Δ=0，該方程在實數域內有兩個相等的實數根:；
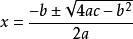公式法若Δ<0，該方程在實數域內無解，但在虛數域內有兩個共軛復根，為。
證明
任何一元二次方程組都能寫成一般形式：
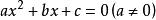公式法①
運用配方法能否解出①呢？
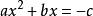公式法移項，得.
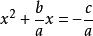公式法二次項係數化1，得.
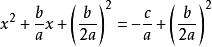公式法配方
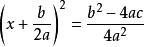公式法即②
∵a≠0
∴4a >0
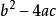公式法的值有三種情況：
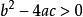公式法1）
由②得
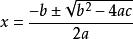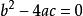公式法∴
公式法2)
由②得
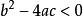公式法3)
由②得<0
∴實數範圍內，此方程無解
判別式
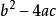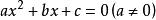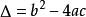公式法 公式法 公式法一般的，式子叫做方程的 判別式，通常用希臘字母Δ表示它，即 .
求根公式
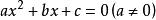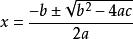公式法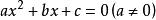 公式法 公式法綜上所述，當Δ≥0時，方程的實數根可寫為的形式，這個式子叫做一元二次方程的 求根公式,通過求根公式可知，一元二次方程的根只可能有 兩個（有相同的算兩個）。
注意事項
一定不會出現不能用公式法解一元二次方程的情況。
但在能直接開方或者因式分解時最好用直接開方法和分解因式法。
