基本介紹
試用條件
例子：3x²+5xy－2y²+x+9y－4，對應的三階矩陣為：
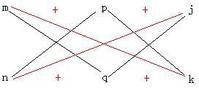
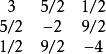雙十字相乘法上面這個矩陣值為0，那么這個二元二次多項式可以用雙十字相乘法。
適用狀況
雙十字相乘法是一種因式分解方法。對於型如 Ax²+Bxy+Cy²+Dx+Ey+F 的多項式的因式分解，常採用的方法是待定係數法。這種方法運算過程較繁。對於這問題，若採用“雙十字相乘法”（主元法），就能很容易將此類型的多項式分解因式。
例子
例：3x²+5xy－2y²+x+9y－4=（x+2y－1）（3x－y+4）
因為3=1×3，－2=2×（－1），－4=（－1）×4，
而1×（－1）+3×2=5，2×4+（－1）（－1）=9，1×4+3×（－1）=1
雙十字相乘的遷移
分解二次五項式
要訣：把缺少的一項當作係數為0，0乘任何數得0，
例：ab+b^2+a－b－2
=0×1×a^2+ab+b^2+a－b－2
=（0×a+b+1）（a+b－2）
=（b+1）（a+b－2）
分解四次五項式
提示：設x^2=y，用拆項法把cx^2拆成mx^2與ny之和。
例：2x^4+13x^3+20x^2+11x+2
=2y^2+13xy+15x^2+5y+11x+2
=（2y+3x+1）（y+5x+2）
=（2x^2+3x+1）（x^2+5x+2）
=（x+1）（2x+1）（x^2+5x+2）
簡單方法
因式分解法
分解二次三項式時，我們常用十字相乘法．對於某些二元二次六項式（ax^2+bxy+cy^2+dx+ey+f），我們也可以用十字相乘法分解因式．
例如，分解因式2x^2-7xy-22y^2-5x+35y-3．我們將上式按x降冪排列，並把y當作常數，於是上式可變形為
2x^2-（5+7y)x-（22y^2-35y+3），
可以看作是關於x的二次三項式．
對於常數項而言，它是關於y的二次三項式，也可以用十字相乘法，分解為
即
-22y^2+35y-3=（2y-3）（-11y+1）．
再利用十字相乘法對關於x的二次三項式分解
所以
原式=〔x+（2y-3）〕〔2x+(-11y+1）〕
=(x+2y-3）（2x-11y+1）．
（x+2y）（2x-11y)=2x2-7xy-22y2；
（x-3）（2x+1）=2x2-5x-3；
（2y-3）（-11y+1）=-22y^2+35y-3．
這就是所謂的雙十字相乘法．
用雙十字相乘法對多項式ax^2+bxy+cy^2+dx+ey+f進行因式分解的步驟是：
⑴用十字相乘法分解ax^2+bxy+cy^2，得到一個十字相乘圖（有兩列）；
⑵把常數項f分解成兩個因式填在第三列上，要求第二、第三列構成的十字交叉之積的和等於原式中的ey，第一列、第三列構成的十字交叉之積的和等於原式中的dx。
求根法
我們把形如anx^n+a(n-1）x^(n-1）+…+a1x+a0(n為非負整數）的代數式稱為關於x的一元多項式，並用f(x），g(x），…等記號表示，如：
f(x)=x^2-3x+2，g(x)=x^5+x^2+6，…，
當x=a時，多項式f(x）的值用f(a）表示．如對上面的多項式f(x)
f⑴=12-3×1+2=0；
f(-2）=(-2）^2-3×（-2）+2=12．
若f(a)=0，則稱a為多項式f(x）的一個根．
定理1（因式定理） 若a是一元多項式f(x）的根，即f(a)=0成立，則多項式f(x）有一個因式（x-a）。
根據因式定理，找出一元多項式f(x）的一次因式的關鍵是求多項式f(x）的根．對於任意多項式f(x），要求出它的根是沒有一般方法的，然而當多項式f(x）的係數都是整數時，即整係數多項式時，經常用下面的定理來判定它是否有有理根。
