四色定理論文手稿
 1
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 9
9 10
10 11
11 12
12 13
13 14
14 15
15 16
16 17
17 18
18 19
19 20
20 21
21 22
22 23
23 24
24 25
25 26
26 27
27 28
28 29
29 30
30 31
31 32
32 33
33 34
34 35
35定理簡介
 四色猜想
四色猜想這是一個拓撲學問題,即找出給球面(或平面)地圖著色時所需用的不同顏色的最小數目。著色時要使得沒有兩個相鄰(即有公共邊界線段)的區域有相同的顏色。1852年英國的格思里推測:四種顏色是充分必要的。1878年英國數學家凱利在一次數學家會議上呼籲大家注意解決這個問題。直到1976年,美國數學家阿佩哈爾、哈肯和考西利用高速電子計算機運算了1200個小時,才證明了格思里的推測。四色問題的解決在數學研究方法上的突破,開闢了機器證明的美好前景。
1994年中國曾邦哲在《結構論》中從系統論觀點將其命題轉換為“四色定理”等價於“互鄰面最大的多面體是四面體”的問題,也就是點之間相互的聯線超過3的是立體,而每增加一個點或表面時必然分割一條線或一個面,也就使分割開的不互鄰面或聯線可以重複使用一種顏色;因此,增加一個面同時也增加一次可重複使用同一種顏色。
定律概述
 四色猜想
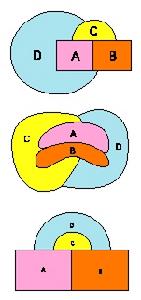
四色猜想1,提出“ 二 接壤國圖形用不同的二種色區分,稱接壤 隔離 ”的概念。再提出 引理: 二 種色不能為三互接壤包圍國 圖形接壤隔離填色。可方便將地球表面上任何多個 任意 接壤包圍國 圖形的 隔離填色 ,視為由 兩兩 接壤包圍國 圖形 接壤 隔離填色的形式。
2, 後提出以 引理 為據,用一組二種色與其 非—— 另組色,對接壤包圍國 圖形互動 接壤 隔離 填 色:不斷用一組二種色 接壤隔離填色先分解後 包圍 ;用另組空白 接壤 隔離補充 包圍和分解;一組不能 接壤 隔離時用 另 組空白;另組空白不能 接壤 隔離時用 一 組;空白最後隔離 填 色,從各所用空白 接壤包圍國 圖形組合的一末端國圖形起,按順序完成 接壤 隔離填色的動態隔離法。
3, 然後按數學歸納法 證明 動態隔離法: 各所用一組二種色 接壤 隔離 填 色的 國 圖形已是用二種色,而各所用 另 組空白的 接壤包圍國 圖形,最後隔離 填 色僅用二色就可完成,故 證明地球表面上任何多個 任意 接壤包圍國 圖形 可 用不超過四種色完成隔離 填 色 ,證明 四色猜想 成立。
4, 而後又進一步用反證法證明: 動態隔離法 是地球表面上任何多個 任意 接壤包圍國 圖形,用不超過四種色完成隔離 填 色的充分必要條件,且部分隔離 國 圖形顏色可選定。
定理的誕生過程
 四色猜想
四色猜想世界近代三大數學難題之一(另外兩個是費馬定理和哥德巴赫猜想)。四色猜想的提出來自英國。1852年,畢業於倫敦大學的弗南西斯·格思里(Francis Guthrie)來到一家科研單位搞地圖著色工作時,發現了一種有趣的現象:“看來,每幅地圖都可以用四種顏色著色,使得有共同邊界的國家著上不同的顏色。”,用數學語言表示,即“將平面任意地細分為不相重迭的區域,每一個區域總可以用1,2,3,4這四個數字之一來標記,而不會使相鄰的兩個區域得到相同的數字。”這個結論能不能從數學上加以嚴格證明呢?他和在大學讀書的弟弟格里斯決心試一試。兄弟二人為證明這一問題而使用的稿紙已經堆了一大疊,可是研究工作沒有進展。
1852年10月23日,他的弟弟就這個問題的證明請教他的老師、著名數學家德·摩爾根,摩爾根也沒有能找到解決這個問題的途徑,於是寫信向自己的好友、著名數學家哈密爾頓爵士請教。哈密爾頓接到摩爾根的信後,對四色問題進行論證。但直到1865年哈密爾頓逝世為止,問題也沒有能夠解決。
1872年,英國當時最著名的數學家凱利正式向倫敦數學學會提出了這個問題,於是四色猜想成了世界數學界關注的問題。世界上許多一流的數學家都紛紛參加了四色猜想的大會戰。1878~1880年兩年間,著名的律師兼數學家肯普和泰勒兩人分別提交了證明四色猜想的論文,宣布證明了四色定理,大家都認為四色猜想從此也就解決了。
11年後,即1890年,數學家赫伍德以自己的精確計算指出肯普的證明是錯誤的。不久,泰勒的證明也被人們否定了。後來,越來越多的數學家雖然對此絞盡腦汁,但一無所獲。於是,人們開始認識到,這個貌似容易的題目,其實是一個可與費馬猜想相媲美的難題:先輩數學大師們的努力,為後世的數學家揭示四色猜想之謎鋪平了道路。
進入20世紀以來,科學家們對四色猜想的證明基本上是按照肯普的想法在進行。1913年,伯克霍夫在肯普的基礎上引進了一些新技巧,美國數學家富蘭克林於1939年證明了22國以下的地圖都可以用四色著色。1950年,有人從22國推進到35國。1960年,有人又證明了39國以下的地圖可以只用四種顏色著色;隨後又推進到了50國。看來這種推進仍然十分緩慢。電子計算機問世以後,由於演算速度迅速提高,加之人機對話的出現,大大加快了對四色猜想證明的進程。1976年,在J. Koch的算法的支持下,美國數學家阿佩爾(Kenneth Appel)與哈肯(Wolfgang Haken)在美國伊利諾斯大學的兩台不同的電子計算機上,用了1200個小時,作了100億判斷,終於完成了四色定理的證明。四色猜想的計算機證明,轟動了世界,當時中國科學家也有在研究這原理。它不僅解決了一個歷時100多年的難題,而且有可能成為數學史上一系列新思維的起點。
證明方法
證明方法將地圖上的無限種可能情況減少為1,936種狀態(稍後減少為1,476種),這些狀態由計算機一個挨一個的進行檢查。這一工作由不同的程式和計算機獨立的進行了復檢。在1996年,Neil Robertson、Daniel Sanders、Paul Seymour和Robin Thomas使用了一種類似的證明方法,檢查了633種特殊的情況。這一新證明也使用了計算機,如果由人工來檢查的話是不切實際的。
韓世君 利用三角形和數學歸納法證明
將平面圖的不相連點使其相連(這樣增加著色難度),形成有許多三角形相連的平面圖,根據三角形的穩定性,利用數學歸納法,平面圖進行著色最多需4種顏色。
定理
在平面圖中,對不同頂點進行著色,相鄰頂點著不同顏色,不相鄰頂點著相同顏色,則最多需4種顏色。
證明
在平面圖中,不在同一直線上的三點決定一個平面,那么三點構成的三角形是平面圖中最基本、最簡單、最穩定、密閉的圖形。
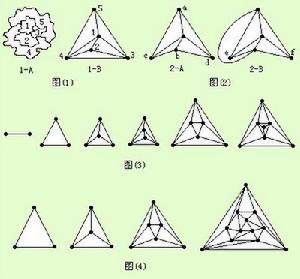
由於在對地圖著色過程中不考慮圖的具體形狀只考慮點是否相鄰,將平面圖的不相連點使其相連(這樣增加著色難度),形成有許多三角形相連的平面圖(三點以下肯定成立)。如圖1:添加輔助線(不相鄰的點使其相鄰,這樣就增加了著色的色數,有利於證明),將圖1分解為4個△ABC。
在平面圖中的無數點中,任取相鄰三點構成各點相鄰的△ABC(見圖2),則需3種顏色ABC,在平面圖中再任取一點D與ABC三點相鄰,同時D又與ABC三點相連後形成三角形。任取一點E與A、B、C、D四色相連,E必與四色之一色相同即E點在△ABD中與C色相同、在△ACD中與B色相同、在△BCD中與A色相同、在△ABC外與D色相同,E與另外三色相連形成新的三角形。
在三角形的三點之外任取一點只有在三角形的內部和外部兩種情況且這兩種情況的點不會相鄰,該點最多與三角形的三點相連且又形成新的三角形。
繼續選取一點進行著色,該點同樣最多與三角形的三點相連且又形成新的三角形,該點至少為四色中的一色。逐點(第n點)著色至將所有點(第n+1點)著色只須A、B、C、D四色其中一色。
圖的著色方法:任意一張地圖,將孤立的點用一種顏色著色(A色),不能形成密閉圖形的相連的點用兩種顏色(A、B色)。將剩餘的點不相連的用虛線使其相連形成許多三角形,完全不相連的圖不進行相連。任取相連三點著三種顏色(A、B、C色),再取與其相連的點,如果與A、B、C三色的點都相連著D色,否則著與其不相連的其中一色,用虛線相連的點可以用同一種顏色也可以用兩種顏色,依次取與著色的點相連的點用以上方法進行著色。這樣對所有的點進行著色最多用四色(A、B、C、D色)。
定理的重要
四色定理是第一個主要由計算機證明的理論,這一證明並不被所有的數學家接受,因為它不能由人工直接驗證。最終,人們必須對計算機編譯的正確性以及運行這一程式的硬體設備充分信任。
缺乏數學應有的規範成為了另一個方面;以至於有人這樣評論“一個好的數學證明應當像一首詩——而這純粹是一本電話簿!”
四色定理成立區劃意義重大
摘要:地圖著色只用四色即可區劃相鄰地區的問題,是近代三大數學難題之一。求證四色問題,需要數學,地理學,區劃學等各方面的知識。我在創新區劃學說,並取得重大發明之後,創新性思維和系統性論證四色定理成立。同時為我區劃創新的科學性及其技術套用,奠定了科學基礎。
用地圖區劃,幾何求證,圖論推倒,圖形拼合,地理分析綜合論證四色定理成立,互相可以聯想,參證,並發現許多奧妙和定理。由自然數集奇偶性,必然導致二色偶區環圖,三色奇區環圖,三色三區環圖具有環閉性,四色區環圖無必然性,五色區環圖無必然性,因而四色定理成立。進而猜想三維空間五色定理成立。
本論文實際上是綜合多學科進行數學難題論證的結果。使得四色定理的證明過程由淺入深,由簡入繁,由一至無窮,由直觀入抽象。因此具有很大的實用價值和套用範圍。教育工作者可以啟迪大中小學生提高對數和形的深刻認識。科技工作者可以正確套用定理進行工程設計和規劃制定。尤其是區劃學科得到廣泛套用。使地圖,地理,行政,組織,軍隊,交通,旅遊,自然,經濟,城建,工程,各項分類分級區劃都按最優原則合理安排,從而大大提高全國人民的工作效率。
關鍵字:圖,奇,偶,區劃,相鄰,相隔,唯一性,環閉性,二色偶環,三色奇環。
定理綜合:由自然數集奇偶性質,推論定理如下:
定理一:一點偶線形成二色2k區環圖。定理二:一點奇線形成三色2k+1區環圖。定理三:一點或面外三色三區環圖,因相鄰不隔具有環閉性。定理四:四區環圖必有二圖相隔可用同色無環閉性。定理五:四色區環圖無必然性,不都成相鄰不隔關係。定理六:二交點三線“工”形相鄰四區環圖只用三色區劃。定理七:偶點圖相鄰各色區劃。定理九:四色四區奇面三環圖,因相鄰不隔具有唯一性。定理十:二維四方圖的一維環閉合形成三色環,必使另一維環相隔。定理十一:中環二邊內環和外環相隔可以使用相同三色。定理十二:內中外三環之間任一區圖不會相鄰四色區圖。定理十三:任一圖同時相鄰四圖,必有二圖相隔可用同色。定理十四:任二圖同時相鄰在三色環中必會形成二圖相隔可用同色。定理十五:五色區劃圖無必然性。不都成相鄰不隔關係。定理十六:四色定理成立具有必然性,這是系統歸納的結果。
結論解密:圖內多點可作一組平行線,形成左右區劃二色鄰隔環,又使某一圖相鄰左右二圖相鄰相隔,並且在圓環面上因奇數形成三色區劃。同時具有環閉性。地球面上的經線可作為平行線繞地球一周成環。各經線又在南北極交於圓心。
圖外多點可做一組同心圓環線,形成內外相鄰二色區劃,又使某一圓環圖相鄰內外二圓環圖形成內中外相鄰相隔。但圓環線的三色環閉性,使得內外二環相隔可使用相同三色環。地球面上的緯線可作為同心圓環線不再成環,分別在南北極終止於圓心。
這就是球面二維四方相對二個鄰隔環互有不同的原因。其中一組鄰隔環閉合必使另一組鄰隔環相隔。這就是五圖之間,其中一組三圖形成三色環閉性。必使另二圖相隔可用同色的原因。也是任何一圖至多相鄰三色環,不會相鄰四色環的原因。因而使得五色定理不具有必然性,而在三維空間成立具有必然性,所以地圖區劃四色定理成立。
定理記載
地圖四色定理最先是由一位叫古德里(Francis Guthrie)的英國大學生提出來的。德•摩爾根(A,DeMorgan,1806~1871)1852年10月23日致哈密頓的一封信提供了有關四色定理來源的最原始的記載。他在信中簡述了自己證明四色定理的構想與感受。一個多世紀以來,數學家們為證明這條定理絞盡腦汁,所引進的概念與方法刺激了拓撲學與圖論的生長、發展。1976年美國數學家阿佩爾(K.Appel)與哈肯(W.Haken)宣告藉助電子計算機獲得了四色定理的證明,又為用計算機證明數學定理開拓了前景。以下摘錄德•摩爾根致哈密頓信的主要部分,譯自J. Fauve1 and J.Gray(eds.),The History of Mathematics :A Reader,pp. 597~598。德·摩爾根致哈密頓的信(1852年10月23日)
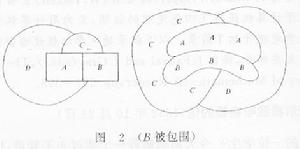
現在仍不甚了了的事實。他說如果任意劃分一個圖形並給各部分著上顏色,使任何具有公共邊界的部分顏色不同,那么需要且僅需要四種顏色就夠了。下圖是需要四種顏色的例子。現在的問題是是否會出現需要五種或更多種顏色的情形。就我目前的理解,若四個不訂分割的區域兩兩具有公共邊界線,則其中三個必包圍第四個而使其不與任何第五個區域相毗鄰。這事實若能成立,那么用四種顏色即可為任何可能的地圖著色,使除了在公共點外同種顏色不會出現畫出三個兩兩具有公共邊界的區域ABC,那么似乎不可能再畫第四個區域與其他三個區域的每一個都有公共邊界,除非它包圍了其中一個區域。但要證明這一點卻很棘手,我也不能確定問題複雜的程度一對此您的意見如何呢?並且此事如果當真,難道從未有人注意過嗎?我的學生說這是在給一幅英國地圖著色時提出的猜測。我越想越覺得這是顯然的事情。如果您能舉出一個簡單的反例來,說明我像一頭蠢驢,那我只好重蹈史芬克斯的覆轍了……。
色數規律
萬有圖形色數規律
中華民族曾是大自然鍾秀的國土和人民,所以很早就有了"道為一,一分二,二生三,三化萬物"的哲理思想。我以深思發現:“奇偶成一,一分為二,二和生三、三變化四、四四進位,層層最佳化,和諧發展,天道自然。”我進而很自然地用完全數學歸納法,證明了人類進行跨世紀猜想論證的世界科學難題,即地圖區劃四色問題,使其成為真奇美的四色定理。
人們長期以來把周易理論:“太極分二儀,二儀分四象,四象分八卦”。看作二進位制。我則深入研究把其看作自然空間不同維數的最優進位單位。由此我發現:宇宙時空最優進位制是,一維的二進位制,二維的四進位制,三位的八進位制,四維的十六進制。在其不同維數領域有其特優的實用價值。
我科學地證明:一色區劃圖在0維原點系統成立是太極元一色定理。二色區劃圖在一維曲線系統成立是羅盤儀二色定理。四色區劃圖在二維曲面系統成立是地球圖四色定理。八色區劃圖在三維空間系統成立是萬物象八色定理。十六色區劃圖在四維時空系統成立是宇宙規十六色定理。由此成為萬有曲面的拓撲不變色數標準模型。我就此創新了人類千年以來夢寐以求的宇宙萬物曲面分類定理,相對證明數學大師龐加萊猜想是個錯誤命題,因而無解。同時展示了完美的萬有圖形色數規律。
我還發現:物理色譜:一維二色分黑白,二維四色分紅黃藍黑,三維八色分紅橙黃綠青藍紫黑。而在0維系統為混沌中性一色為灰。因為事物總是隨時間和空間的位置的改變而作始終運動,所以八色彩也因此始終形成不同深淺顏色分十六色及其倍數色。我把圖形色數進行了有機有序的完美統一。
我的萬有圖形色數理論構成了系統科學的區劃論,思想的協調論,行動的最佳化論。因為其產生於人類千百年的實踐經驗和科學文化知識結累,以及本人數十年的追索研究。因此一旦上升為定理,必然形成自然科學人文知識的完美和諧的標準模型。將象羅盤一樣統一人們的思想和行動以和諧發展,從而成為一種科學規儀。
我在自然時空最優境界的研究成果,展示了地球和宇宙的各維圖形色數的系統區劃分類定理。其統一色數推導公式是:N=2+K,即N色數=2奇偶數+K維數。這是美妙的構思,劃時代的貢獻。相比愛因斯坦的質能轉換公式E=mc2,剛好一世紀。其也必將產生世紀性意義和影響,永遠燦爛輝煌,閃亮於全中國,造福於全人類。
定律奧秘
全球眾多的數學家和科學愛好者,進行跨世紀猜想論證的四色定理。本人因發明了鄰隔環思想系統區劃論,並根據數學完全歸納法進行論證,終於獲得了合理的證明,從而揭開了最迷人的形圖色數,在二維可平面區劃的奧秘。
用地圖區劃,幾何求證,圖論推導,圖形拼合,地理分析,綜合論證了四色定理成立。相互可以聯想,參證,並發現許多地球的奧秘和定理。由自然數的奇偶性,必然導致一色一區劃圖,二色偶區劃環圖,三色奇區環圖,三色三區一環圖具有簡單環閉性,四色四區二環圖有複式環閉性,五色區劃圖無必然性。因而四色定理在二維曲面系統必然成立。進而科學猜想五色定理在三維空間成立。
定理1. 1區劃0環在一維可直線曲面圖為1色圖。
定理2. n區劃0環在一維可直線曲面圖為2色圖。
定理3. 奇區劃1環在二維可平面曲面圖為3色圖。
定理4. n區劃2環在二維可平面曲面圖為4色圖。
定理5. 偶點圖區劃2色偶區圖為3色圖。
定理6. 奇點圖區劃3色奇區圖為4色圖。
定理7. 1圖區劃4色2環圖仍為4色圖。
定理8. 2圖區劃3色1環圖僅為4色圖。
定理9. 3色3區1環圖各區相鄰不隔有單環閉性。
定理10. 4色4區2環圖各區相鄰不隔有復環閉性。
定理11. 4方圖的1環成3色環必相隔另1環。
定理12. 相隔的2環可使用相同的3色環區圖。
定理13. 內中外3環任1圖僅相鄰3色區劃圖。
定理14. 2色區劃圖在一維直線系統有必然性成立二色定理。
定理15. 4色區劃圖在二維平面系統有必然性成立四色定理。
定理16. 5色區劃圖在二維平面系統無必然性而在三維成立。
宇宙萬物圖的奧秘——十六色定理
羅永海 中國上海市黃浦區黃河路215弄54支弄22號
摘要: 一百年前數學大師龐加萊創造了代數拓撲學,並且提出了聞名的猜想以求萬有曲面分類定理。他先斷言:如果兩個閉流形有相同的Betti數和撓係數,它們就同胚。但在三維流形他增加單連通作為條件,即:每一個單連通的閉的能定向的三維流形同胚於三維球。龐加萊猜想曾被推廣成:每一個單連通的閉的n維流形,如果具有n維球的Betti數和撓係數,它就同胚於n維球。推廣的各維猜想已被證明。只剩n=3的龐加萊猜想成為乾年難題。因為人類夢寐以求的是對宇宙萬有曲面進行分類。本人論證宇宙萬有曲面色數分類定理,創造萬有曲面的拓撲不變色數正確模型。從而相對證明龐加萊猜想是個錯誤命題,因而無可能解。
關鍵字:圖、環、圈、區劃、曲面、聯通、二維、三維、四維、
定理1. 1區劃0環在一維曲面圖為1色圖。
定理2. 2區劃0環在一維曲面圖為2色圖。
定理3. 3區劃1環在二維曲面圖為3色圖。
定理4. 0圈1聯通2環二維曲面圖為4色圖。
定理5. 1圈2聯通3環三維曲面圖為5色圖。
定理6. 2圈3聯通4環三維曲面圖為6色圖。
定理7. 3圈4聯通5環三維曲面圖為7色圖。
定理8. 4圈5聯通6環三維曲面圖為8色圖。
定理9. 2色區劃圖在一維直線系統有必然性成立二色定理。
定理10. 4色區劃圖在二維平面系統有必然性成立四色定理。
定理11. 8色區劃圖在三維立面系統有必然性成立八色定理。
定理12. 16色區劃圖在四維超面系統有必然性成立十六色定理。
定理13. 4圈5聯通在三維空間相鄰不隔有復環閉性。
定理14. 5圈區劃在三維空間因相隔同色性仍為8色圖。
定理15. 9色區劃圖在三維系統無必然性而在四維成立。
定理16. 二維和三維空間萬有曲面圖有K+2色統一性。
宏偉的原創性科學發現和發明——萬有圖形色數
羅永海 中國上海市黃浦區黃河路215弄54支弄22號
定理標準
偉大的中國創造了宏偉的四大發明。羅盤為人類進步指明了方向,火藥把載人太空飛行器射向太空,造紙和印刷把媒體覆蓋全球。後三項大發明已有數百萬人們投身於兩彈一星工程和電腦以及網際網路系統,並且不斷拓展而獲得巨大成功,由此極大地推進了人類的巨大生產力。但人類則為首項大發明羅盤在二維和三維空間以至四維時空的拓展,以求證明地球區劃四色定理和宇宙萬有色數分類定理,卻百思不解,以至無法求得地球區劃四色奧秘,乃至宇宙萬有色數奧秘。
本世紀伊始,在巴黎召開的國際數學大會上,美國數學界已向全世紀公民宣布,懸賞100萬美元的千年數學難題,以求破解龐加萊猜想,最終求得宇宙萬有色數分類定理。2005年中國數學網站舉行的世界最迷人的數學難題評選。最終評選出數論“哥德巴赫猜想”,和圖論“四色猜想”為最迷人數學難題前兩名。而後者,我以完全數學歸納法證明其成立四色定理,並且其真是我們人類唯一的家園—地球的色數奧秘。同時也證明美國人的電腦以枚舉歸納法論證四色定理,只是徒有虛名。不可避免圖集僅僅是一個構形。命名其為羅華三色環圓,並與羅中金三角點成為一對雙生子。因為三色環圓具有特殊的封密性和完美性,任何幾何圖都最終可分為三角形圖,而三角形圖再分也是如此不可避免構圖。
格物致知,天道自然。這才是檢驗定理的標準。因此,只要翻開地圖就可智慧發現到處都是金三角點和三色環圓。自然數奇偶性為其完全歸納證明。所以,紅黃綠藍黑白灰,最簡單的點線面,構成了既奇巧複雜,又和諧分級的地圖構形。這就是人類所要最終尋求的地球表面構形的奧妙,乃至拓展到宇宙萬有構形的奧秘。同時也把圖形色數各學科和諧統一了。
聯合國提倡的“地球國際年”——“認識地球和諧發展”。本人創新了宇宙萬有圖形色數規律:其在一維直線是二色定理,在二維曲面是四色定量,在三維空間是八色定理,在四維時空是十六色定理。我把偉大發明羅盤指南針拓展為地球區劃圖,萬物八卦象,宇宙色數規。並使中國古代樸素的周易理論:“太極分二儀,二儀分四象,四象分八卦。”賦予了創新的內容,使其成為系統科學區劃論,其本質就是人們的路線圖和領導的規劃圖。源於自然規律,人類關係和國家區劃,凝聚成思想協調論和行動最佳化論。博大精深的萬有圖形色數規律,具有指明方向並且顯示和諧標準的偉大意義。
然而兩年來,盡了所有精力,仍無法通過國家各大部委和科研院校以及報刊媒體,來把如此重要的科學研究成果,敬獻給祖國人民和黨政領導。這一耽擱已給祖國帶來很大損失,畢竟許多的工程實踐和物質建設,仍還是在並不文明和科學地進行著。因此我希望人們在為萬有圖形色數規律和定理的推廣和實行的過程中,都能儘自己的一份貢獻,並享受其真理的智慧的光輝。
有詩為證: 圖內圖外圖環圖,四色區劃顯神奇。
系統鄰隔二維分,東西南北三色齊。
多少奇巧繁化簡,大小和諧類變級。
創優環球新區劃,精彩奧秘在偶奇。
理論證明
2006年4月,正在主講"神經網路"的科大信息學院陳賢富老師突然被自己在黑板上隨便畫的 5 階Hopfield聯想記憶模型"驚"了片刻.為何5 階Hopfield聯想記憶模型(K5)具有奇特的、"立體的美感"?! 被這一瞬間的靈感觸發, 聯想起著名的四色問題, 陳賢富博士針對任意簡單連通圖的k染色問題展開了持續的思索和研究, 終於提出了基於不可約肯普鏈團的k色猜想, 並於最近徹底攻克"格思里四色猜想"的數學證明問題. 此外,在機器證明方面,陳賢富博士也提出了一個將人類卓越的歸納推理能力與計算機高速的計算能力相結合的證明四色猜想的新方法。基本思路是讓機器證明一個規模相當小的染色特例問題(在個人電腦上可以簡單方便地驗證),再運用數學歸納法,將機器證明的特例歸納推廣到一般情形。真可謂"殊途同歸,一通百達!"
中國科學技術大學信息科學學院陳賢富博士已於一個月前徹底解決世界數學名題----四色猜想的理論證明問題! 2008年3月19日, 陳賢富博士在中國科學技術大學首次報告四色猜想的理論證明。
