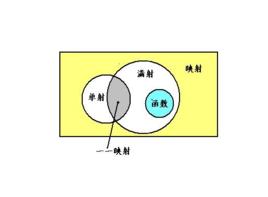
例子反例
對任一集合X,X上的恆等函式為單射的。
函式f : R → R,其定義為f(x) = 2x + 1,是單射的。
函式g : R → R,其定義為g(x) = x^2,不是單射的,因為g(1) = 1 = g(−1)。但若將g的定義域限在非負數[0,+∞)內或非正數(-∞,0]內,則g是單射的。
指數函式exp:R → R+:x → e^x(e的x次方)是單射的。
自然對數函式ln:(0,+∞) → R:x → ln x是單射的。
 單射
單射函式g : R → R,其定義為g(x) = x^3 − x,不是單射的,因為 g(0) = g(1)。
更一般地說,當X和Y都是實數線 R',則單射函式f : R → R為一絕不會與任一水平線相交超過一點的圖。
可逆函式
另一單射函式的定義為其作用可取消的函式。更精確地說,f : X → Y為單射,若存在一函式g : Y → X,使得對所有X內的x,g(f(x)) = x,亦即g o f 等同於X上的恆等函式。
注意,g不一定是一f的完全反函式,因為其他順序的複合f o g不一定是在X上的恆等函式。
事實上,將一單射函式f : X → Y變成一雙射函式,只需要將其陪域Y替換成其值域J = f(X)就行了。亦即,令g : X → J,使其對所以X內的x,g(x) = f(x);如此g便為單射的了。確實,f可以分解成inclJ,Yog,其中inclJ,Y來由J至Y的內含映射。
其他性質
若f和g皆為單射的,則f o g亦為單射的。
若g o f為單射的,則f為單射的(但g不必然要是)。
f : X → Y是單射的若且唯若給定兩函式g、h : W → X會使得f o g = f o h時,則g = h。
若f : X → Y為單射的且A為X的子集,則f −1(f(A)) = A。所以,A可以從其值域f(A)找回。
若f : X → Y是單射的且A和B皆為X的子集,則f(A ∩ B) = f(A) ∩ f(B)。
任一函式 h : W → Y 皆可分解為 h = f o g 其中 f 是單射而 g 是滿射。此分解至多差一個自然同構, f 可以構想為從 h(W) 到 Y 的內含映射。
若 f : X → Y 是單射,則在基數的意義下 Y 的元素數量不少於 X。
若 X 與 Y 皆為有限集,則 f : X → Y 是單射若且唯若它是滿射。
內含映射總是單射。
範疇論的觀點
以範疇論的語言來說,單射函式恰好是集合範疇內的單態射。