定義
 內射模
內射模 內射模
內射模定義一:一個環 上的左模 若滿足以下等價條件,則稱之為 內射模:
 內射模
內射模 內射模
內射模 內射模
內射模 內射模
內射模 內射模
內射模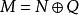 內射模
內射模(1) 若 是左 -模 的子模,則 存在另一個子模 使得 。
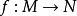 內射模
內射模 內射模
內射模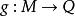 內射模
內射模 內射模
內射模 內射模
內射模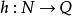 內射模
內射模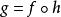 內射模
內射模(2) 若 是單的左 -模映射, 是左 -模映射,則存在 -模映射 使得 。
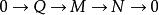 內射模
內射模(3) 任何短正合序列 都分裂。
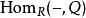 內射模
內射模(4) 函子 為正合函子。
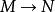 內射模
內射模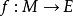 內射模
內射模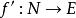 內射模
內射模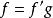 內射模
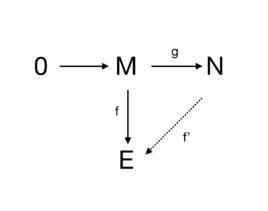
內射模定義二:設R是一個環,E是一個R模。如果對於R模的任意單同態g: ,以及同態 ,f可以擴充為同態 ,使得 ,那么稱E為內射模。
抽象地說,內射模乃是模範疇中的內射對象。
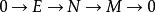 內射模
內射模等價定義:E是內射模若且唯若以E開頭的短正合列 是可裂的。
性質
 內射模
內射模任意一個R模M都同構於內射模的子模,即有內射模E和單同態: 。
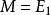 內射模
內射模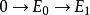 內射模
內射模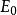 內射模
內射模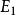 內射模
內射模特別地,若 是一個內射模,則單同態 使得 是的直和項。
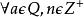 內射模
內射模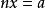 內射模
內射模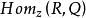 內射模
內射模一個阿貝爾群Q稱為可除的,如果,方程在Q中有解。設R是一個環,Q是一個可除的阿貝爾群,那么是一個內射R模。
內射模的直積(包括無窮直積)仍是內射模,內射模的有限直和仍為內射模。一般而言,內射模的子模、商模或無窮直和並不一定是內射模。
Baer 在其論文中證明了一個有用的結果,通常稱作 Baer 判準:一個左 R-模 Q 是內射模若且唯若定義在任一理想 I 上的態射 I→Q 都能延拓到整個 R 上。
最重要的內射模當屬 Q/Z:它是 Z-模範疇中的 內射上生成元,換言之,這是內射模,而且任何 Z-模皆可嵌入某個 (Q/Z)a次方 中,其中 a 是夠大的基數。由此可知任何 Z-模皆可嵌入某個內射 Z-模。此性質對任意環 R 上的左模都成立,要點在於利用 Q/Z 的特性構造左 R-模範疇中的內射上生成元。