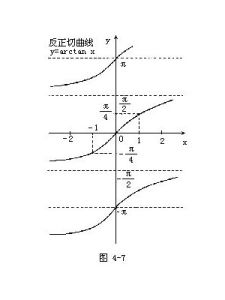
函式簡介
函式y=tanx的反函式叫做反正切函式,記做:y=arctanx.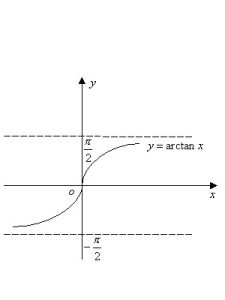 2
2定義域:R
值域:(-π/2,π/2)
單調性:增函式
奇偶性:奇函式
定義
函式y=tanx,x∈(-π/2,π/2)的反函式,記作y=arctanx,叫做反正切函式。反正切函式是反三角函式的一種。同樣,由於正切函式y=tanx在定義域R上不具有一一對應的關係,所以不存在反函式。
注意這裡選取是正切函式的一個單調區間。
性質
定義域:R值域:(-π/2,π/2)
單調性:增函式
奇偶性:奇函式
周期性:不是周期函式
單調性:(-∞,﹢∞)單調遞增
tan(arctana)=a
arctan(-x)=-arctanx
arctanA+arctanB
=arctan(A+B)/(1-AB)
arctanA-arctanB
=arctan(A-B)/(1+AB)
反三角函式在無窮小替換公式中的套用:
當x→0時,arctanx~x
相關條目
數學 函式 奇偶 學科圖像
反正切函式的大致圖像如圖所示,顯然與函式y=tanx,x∈(-π/2,π/2)關於直線y=x對稱,且漸近線為y=π/2和y=-π/2